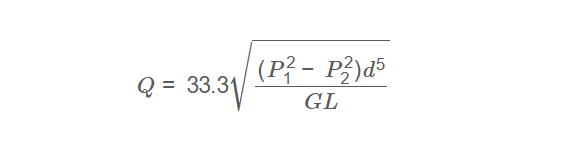Home Back

Gas Flow Rate (Cox Formula for Commercial-Industrial Piping <3 in. Diameter) Calculator

Gas Flow Rate (Cox Formula)

dimensionless

1. What is a Gas Flow Rate (Cox Formula) Calculator?

Definition: This calculator computes the flow rate (\( Q \)) of natural gas in commercial-industrial piping systems for pipes with a diameter less than 3 inches, using the Cox formula.

Purpose: It is used in commercial and industrial gas system design to determine the gas flow rate, aiding in pipe sizing, system efficiency, and ensuring adequate gas supply for smaller-diameter piping applications.

2. How Does the Calculator Work?

The calculator uses the following formula for gas flow rate:

Gas Flow Rate: \[ Q = 33.3 \sqrt{\frac{(P_1^2 - P_2^2) d^5}{G L}} \]

Where:

  • \( Q \): Flow rate (ft³/hr, m³/s)
  • \( P_1 \): Initial absolute pressure (psia, Pa)
  • \( P_2 \): Terminal absolute pressure (psia, Pa)
  • \( d \): Internal diameter of pipe (in., m)
  • \( G \): Specific gravity of gas (dimensionless, typically 0.60 for natural gas)
  • \( L \): Length of pipe (miles, km)

Unit Conversions:

  • Internal Diameter (\( d \)): in., m (1 m = 39.3701 in.)
  • Initial and Terminal Pressure (\( P_1 \), \( P_2 \)): psia, Pa (1 Pa = 0.000145038 psia)
  • Pipe Length (\( L \)): miles, km (1 km = 0.621371 miles)
  • Flow Rate (\( Q \)): ft³/hr, m³/s (1 ft³/hr = 7.86579e-6 m³/s)

Steps:

  • Enter the internal diameter (\( d \)), initial absolute pressure (\( P_1 \)), terminal absolute pressure (\( P_2 \)), specific gravity (\( G \)), and pipe length (\( L \)), and select their units.
  • Convert \( d \), \( P_1 \), \( P_2 \), and \( L \) to in., psia, psia, and miles, respectively.
  • Calculate the flow rate using the formula.
  • Convert the result to the selected unit (ft³/hr or m³/s).
  • Display the result with 5 decimal places, or in scientific notation if the value is greater than 10,000 or less than 0.00001.

3. Importance of Gas Flow Rate Calculation

Calculating the gas flow rate using the Cox formula is crucial for:

  • Commercial-Industrial Gas System Design: Ensures pipes under 3 inches are sized to deliver sufficient gas for applications like small-scale industrial processes or commercial heating.
  • Safety and Efficiency: Prevents pressure drops that could impair system performance or safety in smaller piping systems.
  • System Optimization: Balances pipe size, cost, and gas delivery requirements for efficient operation.

4. Using the Calculator

Examples:

  • Example 1: For \( d = 2 \, \text{in.} \), \( P_1 = 24.7 \, \text{psia} \), \( P_2 = 23.7 \, \text{psia} \), \( G = 0.60 \), \( L = 0.1894 \, \text{miles} \), flow rate in ft³/hr:
    • \( Q = 33.3 \sqrt{\frac{(24.7^2 - 23.7^2) \times 2^5}{0.60 \times 0.1894}} \approx 33.3 \sqrt{\frac{(610.09 - 561.69) \times 32}{0.60 \times 0.1894}} \approx 33.3 \sqrt{\frac{48.4 \times 32}{0.11364}} \approx 33.3 \sqrt{\frac{1548.8}{0.11364}} \approx 33.3 \sqrt{13631.1} \approx 33.3 \times 116.75 \approx 3890 \)
    • Since 3890 < 10000 and > 0.00001, display with 5 decimal places: \( 3890.00000 \)
  • Example 2: For \( d = 0.0508 \, \text{m} \), \( P_1 = 170000 \, \text{Pa} \), \( P_2 = 163000 \, \text{Pa} \), \( G = 0.60 \), \( L = 0.3048 \, \text{km} \), flow rate in m³/s:
    • Convert: \( d = 0.0508 \times 39.3701 \approx 2 \, \text{in.} \)
    • \( P_1 = 170000 \times 0.000145038 \approx 24.656 \, \text{psia} \)
    • \( P_2 = 163000 \times 0.000145038 \approx 23.641 \, \text{psia} \)
    • \( L = 0.3048 \times 0.621371 \approx 0.1894 \, \text{miles} \)
    • \( Q = 33.3 \sqrt{\frac{(24.656^2 - 23.641^2) \times 2^5}{0.60 \times 0.1894}} \approx 33.3 \sqrt{\frac{(607.92 - 558.90) \times 32}{0.11364}} \approx 33.3 \sqrt{\frac{49.02 \times 32}{0.11364}} \approx 33.3 \sqrt{\frac{1568.64}{0.11364}} \approx 33.3 \sqrt{13802.9} \approx 33.3 \times 117.49 \approx 3912.5 \, \text{ft³/hr} \)
    • Convert to m³/s: \( 3912.5 \times 7.86579e-6 \approx 0.03078 \)
    • Since 0.03078 < 10000 and > 0.00001, display with 5 decimal places: \( 0.03078 \)
  • Example 3: For \( d = 1.5 \, \text{in.} \), \( P_1 = 30 \, \text{psia} \), \( P_2 = 28 \, \text{psia} \), \( G = 0.60 \), \( L = 0.5 \, \text{miles} \), flow rate in ft³/hr:
    • \( Q = 33.3 \sqrt{\frac{(30^2 - 28^2) \times 1.5^5}{0.60 \times 0.5}} \approx 33.3 \sqrt{\frac{(900 - 784) \times 7.59375}{0.60 \times 0.5}} \approx 33.3 \sqrt{\frac{116 \times 7.59375}{0.3}} \approx 33.3 \sqrt{\frac{880.875}{0.3}} \approx 33.3 \sqrt{2936.25} \approx 33.3 \times 54.187 \approx 1804.4 \)
    • Since 1804.4 < 10000 and > 0.00001, display with 5 decimal places: \( 1804.40000 \)

5. Frequently Asked Questions (FAQ)

Q: What does gas flow rate in the Cox formula represent?
A: Gas flow rate (\( Q \)) quantifies the volume of natural gas delivered per unit time in commercial-industrial piping systems with diameters less than 3 inches, critical for meeting demand in smaller piping applications.

Q: How can I determine the input parameters?
A: Internal diameter (\( d \)) is obtained from pipe specifications (must be <3 in.). Initial and terminal absolute pressures (\( P_1 \), \( P_2 \)) are measured or designed for the system. Specific gravity (\( G \)) is typically 0.60 for natural gas. Pipe length (\( L \)) is measured in miles or kilometers.

Q: Why is gas flow rate important in commercial-industrial gas system design?
A: It ensures pipes under 3 inches are sized to deliver sufficient gas for safe and efficient operation, optimizing system performance and cost for smaller-scale industrial or commercial applications.

Gas Flow Rate (Cox Formula) Calculator© - All Rights Reserved 2025