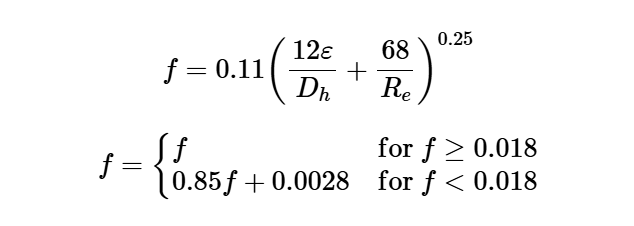1. What is a Friction Factor Calculator?
Definition: This calculator computes the friction factor (\( f \)) for duct flow using the Altshul-Tsal equation, which approximates the Colebrook equation based on duct roughness and Reynolds number.
Purpose: It is used in HVAC design to determine the friction factor for calculating pressure losses in ducts, aiding in efficient duct and fan sizing.
2. How Does the Calculator Work?
The calculator uses the following formula for the friction factor:
Friction Factor:
\[
f = 0.11 \left( \frac{12 \varepsilon}{D_h} + \frac{68}{R_e} \right)^{0.25}
\]
\[
f = \begin{cases}
f & \text{for } f \geq 0.018 \\
0.85 f + 0.0028 & \text{for } f < 0.018
\end{cases}
\]
Where:
- \( f \): Friction factor (dimensionless)
- \( \varepsilon \): Material absolute roughness factor (ft, m)
- \( D_h \): Hydraulic diameter (in., m)
- \( R_e \): Reynolds number (dimensionless)
Unit Conversions:
- Roughness Factor (\( \varepsilon \)): ft, m (1 m = 3.28084 ft)
- Hydraulic Diameter (\( D_h \)): in., m (1 m = 39.3701 in.)
Steps:
- Enter the material absolute roughness factor (\( \varepsilon \)), hydraulic diameter (\( D_h \)), and Reynolds number (\( R_e \)), and select units for \( \varepsilon \) and \( D_h \).
- Convert \( \varepsilon \) to ft and \( D_h \) to in.
- Calculate the initial friction factor using the Altshul-Tsal equation.
- Apply the conditional adjustment based on the initial \( f \).
- Display the result with 5 decimal places, or in scientific notation if the value is greater than 10,000 or less than 0.00001.
3. Importance of Friction Factor Calculation
Calculating the friction factor is crucial for:
- HVAC System Design: Provides the friction factor needed to calculate pressure losses in ducts, guiding fan and duct sizing.
- Energy Efficiency: Optimizes duct design to minimize friction losses, reducing energy consumption.
- System Performance: Ensures proper air flow for effective ventilation and thermal comfort.
4. Using the Calculator
Examples:
- Example 1: For \( \varepsilon = 0.0003 \, \text{ft} \), \( D_h = 24 \, \text{in.} \), \( R_e = 123552 \), friction factor:
- \( f = 0.11 \times \left( \frac{12 \times 0.0003}{24} + \frac{68}{123552} \right)^{0.25} \approx 0.11 \times (0.00015 + 0.0005504)^{0.25} \approx 0.11 \times 0.7004^{0.25} \approx 0.00972 \)
- Since \( f < 0.018 \), \( f = 0.85 \times 0.00972 + 0.0028 \approx 0.008262 + 0.0028 = 0.011062 \)
- Since 0.011062 < 10000 and > 0.00001, display with 5 decimal places: \( 0.01106 \)
- Example 2: For \( \varepsilon = 0.0001 \, \text{m} \), \( D_h = 0.6 \, \text{m} \), \( R_e = 100000 \), friction factor:
- Convert: \( \varepsilon = 0.0001 \times 3.28084 \approx 0.000328084 \, \text{ft} \)
- \( D_h = 0.6 \times 39.3701 \approx 23.62206 \, \text{in.} \)
- \( f = 0.11 \times \left( \frac{12 \times 0.000328084}{23.62206} + \frac{68}{100000} \right)^{0.25} \approx 0.11 \times (0.0001667 + 0.00068)^{0.25} \approx 0.11 \times 0.8467^{0.25} \approx 0.01076 \)
- Since \( f < 0.018 \), \( f = 0.85 \times 0.01076 + 0.0028 \approx 0.009146 + 0.0028 = 0.011946 \)
- Since 0.011946 < 10000 and > 0.00001, display with 5 decimal places: \( 0.01195 \)
- Example 3: For \( \varepsilon = 0.0005 \, \text{ft} \), \( D_h = 12 \, \text{in.} \), \( R_e = 50000 \), friction factor:
- \( f = 0.11 \times \left( \frac{12 \times 0.0005}{12} + \frac{68}{50000} \right)^{0.25} \approx 0.11 \times (0.0005 + 0.00136)^{0.25} \approx 0.11 \times 0.00186^{0.25} \approx 0.01297 \)
- Since \( f < 0.018 \), \( f = 0.85 \times 0.01297 + 0.0028 \approx 0.0110245 + 0.0028 = 0.0138245 \)
- Since 0.0138245 < 10000 and > 0.00001, display with 5 decimal places: \( 0.01382 \)
5. Frequently Asked Questions (FAQ)
Q: What does the friction factor represent?
A: The friction factor (\( f \)) quantifies the resistance to air flow due to duct wall roughness, used to calculate friction losses in HVAC systems.
Q: How can I determine the roughness factor and Reynolds number?
A: The roughness factor (\( \varepsilon \)) is obtained from material property tables (e.g., 0.0003 ft for medium smooth ducts). The Reynolds number (\( R_e \)) is calculated using air velocity, duct diameter, and air properties (e.g., viscosity).
Q: Why is the Altshul-Tsal equation used?
A: It provides a simpler approximation to the Colebrook equation, making it practical for HVAC design while maintaining reasonable accuracy.
Friction Factor (Altshul-Tsal Equation) Calculator© - All Rights Reserved 2025
 Home
Home
 Back
Back