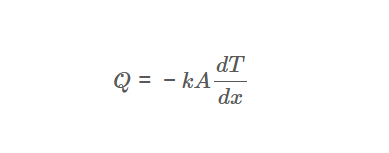Fourier's Law for Thermal Conduction Calculator for HVAC Systems

Fourier's Law for Thermal Conduction Calculator

Thermal Conductivity (\( k \)):

Cross-Sectional Area (\( A \)):

Temperature Gradient (\( \frac{d T}{d x} \)):

1. What is a Fourier's Law for Thermal Conduction Calculator?

Definition: This calculator computes the heat flow rate (\( \dot{Q} \)) through a material via conduction, using Fourier's Law, which relates heat flow to the temperature gradient.

Purpose: It is used in HVAC systems to calculate heat loss through walls, pipes, or other components, ensuring proper insulation design.

2. How Does the Calculator Work?

The calculator uses Fourier's Law for thermal conduction:

Heat Flow Rate: \[ \dot{Q} = -k A \frac{d T}{d x} \]

Where:

\( \dot{Q} \): Heat flow rate (Btu/hr, convertible to W)
\( k \): Thermal conductivity (Btu-ft/hr-ft²-°F, W/m-K)
\( A \): Cross-sectional area normal to heat flow (ft², in², m²)
\( \frac{d T}{d x} \): Temperature gradient (°F/ft, °C/m)

Unit Conversions:

Thermal Conductivity (\( k \)): Btu-ft/hr-ft²-°F, W/m-K (1 W/m-K = 0.577789 Btu-ft/hr-ft²-°F)
Cross-Sectional Area (\( A \)): ft², in² (1 in² = \( \frac{1}{144} \) ft²), m² (1 m² = 10.7639 ft²)
Temperature Gradient (\( \frac{d T}{d x} \)): °F/ft, °C/m (1 °C/m = \( \frac{1.8}{3.28084} \) °F/ft)
Heat Flow Rate (\( \dot{Q} \)): Btu/hr, W (1 Btu/hr = 0.293071 W)

Steps:

Enter the thermal conductivity (\( k \)), cross-sectional area (\( A \)), and temperature gradient (\( \frac{d T}{d x} \)), and select their units.
Convert all inputs to base units (\( k \) to Btu-ft/hr-ft²-°F, \( A \) to ft², \( \frac{d T}{d x} \) to °F/ft).
Calculate the heat flow rate using \( \dot{Q} = -k A \frac{d T}{d x} \), taking the absolute value of the temperature gradient for practical purposes.
Convert the result to the selected unit (Btu/hr, W).
Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Fourier's Law for Thermal Conduction Calculation

Calculating heat conduction is crucial for:

HVAC Design: Determines heat loss through walls, pipes, or ducts, aiding in insulation design.
Energy Efficiency: Helps minimize energy losses by optimizing material selection and thickness.
System Performance: Ensures accurate thermal load calculations for heating and cooling systems.

4. Using the Calculator

Examples:

Example 1: For \( k = 0.2 \, \text{Btu-ft/hr-ft}^2\text{-°F} \), \( A = 10 \, \text{ft}^2 \), \( \frac{d T}{d x} = -5 \, \text{°F/ft} \), heat flow in Btu/hr:
- Heat Flow Rate: \( \dot{Q} = -0.2 \times 10 \times (-5) = 10.0000 \, \text{Btu/hr} \)
Example 2: For \( k = 0.5 \, \text{W/m-K} \), \( A = 1 \, \text{m}^2 \), \( \frac{d T}{d x} = -10 \, \text{°C/m} \), heat flow in W:
- Convert: \( k = 0.5 \times 0.577789 = 0.2888945 \, \text{Btu-ft/hr-ft}^2\text{-°F} \), \( A = 1 \times 10.7639 = 10.7639 \, \text{ft}^2 \), \( \frac{d T}{d x} = -10 \times \frac{1.8}{3.28084} = -5.4863 \, \text{°F/ft} \)
- Heat Flow Rate: \( \dot{Q} = -0.2888945 \times 10.7639 \times (-5.4863) \approx 17.0562 \, \text{Btu/hr} \)
- Convert to W: \( \dot{Q} = 17.0562 \times 0.293071 \approx 5.0000 \, \text{W} \)

5. Frequently Asked Questions (FAQ)

Q: What is Fourier's Law for thermal conduction?
A: Fourier's Law states that the heat flow rate (\( \dot{Q} \)) through a material is proportional to the temperature gradient (\( \frac{d T}{d x} \)), given by \( \dot{Q} = -k A \frac{d T}{d x} \).

Q: Why is thermal conduction important in HVAC systems?
A: It helps calculate heat loss through walls, pipes, or ducts, ensuring proper insulation and efficient system design.

Q: Where can I find thermal conductivity (\( k \)) values?
A: Thermal conductivity values for materials are available in engineering handbooks or material property databases, often specific to temperature and material type.