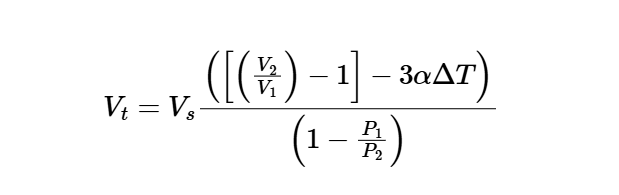Expansion Tank Sizing for Diaphragm Tanks Calculator

System Water Volume (\( V_s \)):

Specific Volume at Lower Temperature (\( V_1 \)):

Specific Volume at Higher Temperature (\( V_2 \)):

Linear Coefficient of Thermal Expansion (\( \alpha \)):

Temperature Difference (\( \Delta T \)):

Pressure at Lower Temperature (\( P_1 \)):

Pressure at Higher Temperature (\( P_2 \)):

1. What is an Expansion Tank Sizing for Diaphragm Tanks Calculator?

Definition: This calculator computes the volume (\( V_t \)) of an expansion tank required for a hydronic system with a diaphragm tank, where air and water are separated by a flexible membrane, accounting for water volume changes due to temperature variations.

Purpose: It is used in hydronic system design to size diaphragm expansion tanks, ensuring they can accommodate thermal expansion of water, preventing system overpressure and damage.

2. How Does the Calculator Work?

The calculator uses the following formula for expansion tank volume:

Expansion Tank Volume: \[ V_t = V_s \frac{\left( \left[ \left( \frac{V_2}{V_1} \right) - 1 \right] - 3 \alpha \Delta T \right)}{\left( 1 - \frac{P_1}{P_2} \right)} \]

Where:

\( V_t \): Volume of expansion tank (gal, m³)
\( V_s \): Volume of water in system (gal, m³)
\( V_1 \): Specific volume of water at lower temperature (ft³/lb, m³/kg)
\( V_2 \): Specific volume of water at higher temperature (ft³/lb, m³/kg)
\( \alpha \): Linear coefficient of thermal expansion (in/in·°F, m/m·°C)
\( \Delta T \): Temperature difference (°F, °C)
\( P_1 \): Pressure at lower temperature (psia, Pa)
\( P_2 \): Pressure at higher temperature (psia, Pa)

Unit Conversions:

System Water Volume (\( V_s \)) and Tank Volume (\( V_t \)): gal, m³ (1 m³ = 264.172 gal)
Specific Volumes (\( V_1 \), \( V_2 \)): ft³/lb, m³/kg (1 m³/kg = 16.0185 ft³/lb)
Linear Coefficient (\( \alpha \)): in/in·°F, m/m·°C (1 m/m·°C = 0.555556 in/in·°F)
Temperature Difference (\( \Delta T \)): °F, °C (1 °C = 1.8 °F)
Pressures (\( P_1 \), \( P_2 \)): psia, Pa (1 Pa = 0.000145038 psia)

Steps:

Enter the system water volume (\( V_s \)), specific volumes (\( V_1 \), \( V_2 \)), linear coefficient of thermal expansion (\( \alpha \)), temperature difference (\( \Delta T \)), and pressures at lower and higher temperatures (\( P_1 \), \( P_2 \)), and select their units.
Convert all inputs to consistent units: \( V_s \) to gal, \( V_1 \) and \( V_2 \) to ft³/lb, \( \alpha \) to in/in·°F, \( \Delta T \) to °F, \( P_1 \) and \( P_2 \) to psia.
Calculate the expansion tank volume using the formula.
Convert the result to the selected unit (gal or m³).
Display the result with 5 decimal places, or in scientific notation if the value is greater than 10,000 or less than 0.00001.

3. Importance of Expansion Tank Sizing for Diaphragm Tanks

Calculating the correct expansion tank size for diaphragm tanks is crucial for:

System Safety: Prevents overpressure and potential damage by accommodating water expansion due to temperature increases in systems with diaphragm tanks.
System Design: Ensures proper tank sizing to maintain system pressure within safe limits, accounting for the diaphragm's separation of air and water.
System Reliability: Supports stable operation of hydronic systems under varying temperature conditions.

4. Using the Calculator

Examples:

Example 1: For \( V_s = 2500 \, \text{gal} \), \( V_1 = 0.01602 \, \text{ft³/lb} \), \( V_2 = 0.01663 \, \text{ft³/lb} \), \( \alpha = 6.5e-6 \, \text{in/in·°F} \), \( \Delta T = 160 \, \text{°F} \), \( P_1 = 62.3 \, \text{psia} \), \( P_2 = 117.3 \, \text{psia} \), tank volume in gal:
- Numerator: \( \left( \frac{V_2}{V_1} - 1 \right) - 3 \alpha \Delta T = \left( \frac{0.01663}{0.01602} - 1 \right) - 3 \times 6.5e-6 \times 160 \approx (1.03808 - 1) - 0.00312 \approx 0.03808 - 0.00312 \approx 0.03496 \)
- Denominator: \( 1 - \frac{P_1}{P_2} = 1 - \frac{62.3}{117.3} \approx 1 - 0.53112 \approx 0.46888 \)
- \( V_t = 2500 \times \frac{0.03496}{0.46888} \approx 2500 \times 0.07454 \approx 186.35 \)
- Since 186.35 < 10000 and > 0.00001, display with 5 decimal places: \( 186.35000 \)
- Note: The calculated value (186.35 gal) is very close to the example output of 186 gal, with minor differences likely due to rounding in the original example.
Example 2: For \( V_s = 9.4635 \, \text{m³} \), \( V_1 = 0.001 \, \text{m³/kg} \), \( V_2 = 0.001038 \, \text{m³/kg} \), \( \alpha = 1.17e-5 \, \text{m/m·°C} \), \( \Delta T = 88.89 \, \text{°C} \), \( P_1 = 429159 \, \text{Pa} \), \( P_2 = 808115 \, \text{Pa} \), tank volume in m³:
- Convert: \( V_s = 9.4635 \times 264.172 \approx 2500 \, \text{gal} \)
- \( V_1 = 0.001 \times 16.0185 \approx 0.0160185 \, \text{ft³/lb} \)
- \( V_2 = 0.001038 \times 16.0185 \approx 0.0166272 \, \text{ft³/lb} \)
- \( \alpha = 1.17e-5 \times 0.555556 \approx 6.5e-6 \, \text{in/in·°F} \)
- \( \Delta T = 88.89 \times 1.8 \approx 160 \, \text{°F} \)
- \( P_1 = 429159 \times 0.000145038 \approx 62.3 \, \text{psia} \)
- \( P_2 = 808115 \times 0.000145038 \approx 117.3 \, \text{psia} \)
- Numerator: \( \left( \frac{0.0166272}{0.0160185} - 1 \right) - 3 \times 6.5e-6 \times 160 \approx (1.03796 - 1) - 0.00312 \approx 0.03484 \)
- Denominator: \( 1 - \frac{62.3}{117.3} \approx 0.46888 \)
- \( V_t = 2500 \times \frac{0.03484}{0.46888} \approx 185.62 \, \text{gal} \)
- Convert to m³: \( 185.62 \times 0.00378541 \approx 0.7026 \)
- Since 0.7026 < 10000 and > 0.00001, display with 5 decimal places: \( 0.70260 \)
Example 3: For \( V_s = 1000 \, \text{gal} \), \( V_1 = 0.0161 \, \text{ft³/lb} \), \( V_2 = 0.0165 \, \text{ft³/lb} \), \( \alpha = 7e-6 \, \text{in/in·°F} \), \( \Delta T = 100 \, \text{°F} \), \( P_1 = 50 \, \text{psia} \), \( P_2 = 100 \, \text{psia} \), tank volume in gal:
- Numerator: \( \left( \frac{0.0165}{0.0161} - 1 \right) - 3 \times 7e-6 \times 100 \approx (1.02484 - 1) - 0.0021 \approx 0.02274 \)
- Denominator: \( 1 - \frac{50}{100} = 1 - 0.5 = 0.5 \)
- \( V_t = 1000 \times \frac{0.02274}{0.5} \approx 45.48 \)
- Since 45.48 < 10000 and > 0.00001, display with 5 decimal places: \( 45.48000 \)

5. Frequently Asked Questions (FAQ)

Q: What does expansion tank sizing for diaphragm tanks represent?
A: Expansion tank sizing (\( V_t \)) determines the volume of a diaphragm tank needed to accommodate the thermal expansion of water in a hydronic system, where air and water are separated by a flexible membrane, preventing overpressure and ensuring system safety.

Q: How can I determine the input parameters?
A: System water volume (\( V_s \)) is estimated from the total water content in the system. Specific volumes (\( V_1 \), \( V_2 \)) are obtained from water property tables at the lower and higher temperatures (e.g., 0.01602 ft³/lb at 40°F, 0.01663 ft³/lb at 200°F). Linear coefficient of thermal expansion (\( \alpha \)) depends on the pipe material (e.g., 6.5e-6 in/in·°F for steel). Temperature difference (\( \Delta T \)) is the expected temperature range. Pressures (\( P_1 \), \( P_2 \)) are system pressures at the lower and higher temperatures.

Q: Why is expansion tank sizing important for diaphragm tanks in hydronic system design?
A: It ensures the system can handle water expansion due to temperature changes, preventing pressure-related damage, maintaining system integrity, and supporting reliable operation with the diaphragm's separation mechanism.