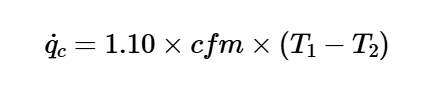1. What is a Cooling Load in Simple Cooling Process Calculator?
Definition: This calculator computes the cooling load (\( \dot{q}_c \)) required in a simple cooling process where the humidity ratio remains constant, and the air temperature is lowered from an entering to a leaving temperature.
Purpose: It is used in HVAC systems to determine the cooling required to lower the temperature of air, aiding in the design and sizing of cooling systems.
2. How Does the Calculator Work?
The calculator uses the following formula for the cooling load:
Cooling Load:
\[
\dot{q}_c = 1.10 \times cfm \times (T_1 - T_2)
\]
Where:
- \( \dot{q}_c \): Cooling load (Btu/hr, convertible to kW)
- \( cfm \): Air flow rate of dry air (ft³/min, m³/s, L/s)
- \( T_1 \): Entering temperature (°F, °C, K)
- \( T_2 \): Leaving temperature (°F, °C, K)
- Constant 1.10: Empirical factor accounting for air density and specific heat (approximately 1.08 to 1.10, depending on conditions; 1.10 is used here as specified)
Unit Conversions:
- Air Flow Rate (\( cfm \)): ft³/min, m³/s (1 m³/s = 2118.88 ft³/min), L/s (1 L/s = 2.11888 ft³/min)
- Temperatures (\( T_1 \), \( T_2 \)): °F, °C (°F = °C × 9/5 + 32), K (°F = (K - 273.15) × 9/5 + 32)
- Cooling Load (\( \dot{q}_c \)): Btu/hr, kW (1 Btu/hr = 0.000293071 kW)
Steps:
- Enter the air flow rate (\( cfm \)), entering temperature (\( T_1 \)), and leaving temperature (\( T_2 \)), and select their units.
- Convert air flow rate to ft³/min and temperatures to °F.
- Calculate the cooling load using the formula.
- Convert the result to the selected unit (Btu/hr or kW).
- Display the result with 5 decimal places, or in scientific notation if the value is greater than 10,000 or less than 0.00001.
3. Importance of Cooling Load Calculation
Calculating the cooling load in a simple cooling process is crucial for:
- HVAC Design: Determines the cooling required to lower air temperature, aiding in the sizing of cooling equipment like chillers and air conditioners.
- Energy Efficiency: Helps optimize energy usage by ensuring the cooling system is appropriately sized for the load.
- System Performance: Ensures the cooling system can achieve the desired leaving temperature for comfort and process requirements.
4. Using the Calculator
Examples:
- Example 1: For \( cfm = 5000 \, \text{ft}^3/\text{min} \), \( T_1 = 75^\circ \text{F} \), \( T_2 = 55^\circ \text{F} \), cooling load in Btu/hr:
- \( \dot{q}_c = 1.10 \times 5000 \times (75 - 55) \)
- \( \dot{q}_c = 1.10 \times 5000 \times 20 = 110000 \, \text{Btu/hr} \)
- Since 110000 > 10000, use scientific notation: \( 1.10000e+5 \)
- Example 2: For \( cfm = 2 \, \text{m}^3/\text{s} \), \( T_1 = 30^\circ \text{C} \), \( T_2 = 20^\circ \text{C} \), cooling load in kW:
- Convert: \( cfm = 2 \times 2118.88 = 4237.76 \, \text{ft}^3/\text{min} \), \( T_1 = (30 \times 9/5) + 32 = 86^\circ \text{F} \), \( T_2 = (20 \times 9/5) + 32 = 68^\circ \text{F} \)
- \( \dot{q}_c = 1.10 \times 4237.76 \times (86 - 68) \)
- \( \dot{q}_c = 1.10 \times 4237.76 \times 18 \approx 83885.23200 \, \text{Btu/hr} \)
- Convert to kW: \( 83885.23200 \times 0.000293071 = 24.58127 \, \text{kW} \)
- Since 24.58127 < 10000 and > 0.00001, display with 5 decimal places: \( 24.58127 \)
- Example 3: For \( cfm = 0.0001 \, \text{ft}^3/\text{min} \), \( T_1 = 25^\circ \text{C} \), \( T_2 = 24^\circ \text{C} \), cooling load in Btu/hr:
- Convert: \( T_1 = (25 \times 9/5) + 32 = 77^\circ \text{F} \), \( T_2 = (24 \times 9/5) + 32 = 75.2^\circ \text{F} \)
- \( \dot{q}_c = 1.10 \times 0.0001 \times (77 - 75.2) \)
- \( \dot{q}_c = 1.10 \times 0.0001 \times 1.8 = 0.000198 \, \text{Btu/hr} \)
- Since 0.000198 < 0.00001, use scientific notation: \( 1.98000e-4 \)
5. Frequently Asked Questions (FAQ)
Q: What is a simple cooling process in HVAC?
A: A simple cooling process in HVAC involves lowering the temperature of air without changing its humidity ratio, typically using a cooling coil or air conditioner.
Q: Why is the constant 1.10 used in the formula?
A: The constant 1.10 is an empirical factor that accounts for the density and specific heat of air, approximating the energy required to cool air under typical conditions (often varies between 1.08 and 1.10; 1.10 is used here as specified).
Q: Why does the humidity ratio remain constant in this process?
A: In a simple cooling process, no moisture is added or removed from the air, so the humidity ratio (mass of water vapor per mass of dry air) remains unchanged while the air temperature decreases.
Cooling Load in Simple Cooling Process Calculator© - All Rights Reserved 2025
 Home
Home
 Back
Back