Home Back

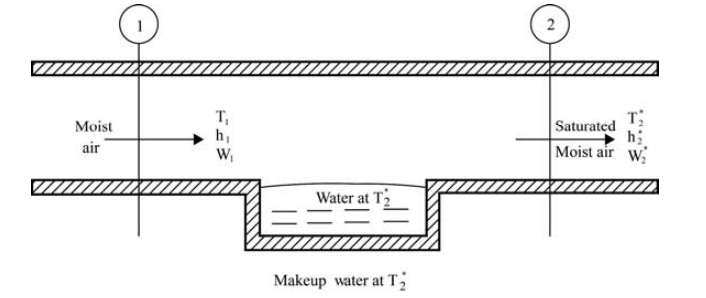
Adiabatic Saturation Process (Humidity Ratio) Calculator

Adiabatic Saturation Process

1. What is an Adiabatic Saturation Process (Humidity Ratio) Calculator?

Definition: This calculator computes the entering humidity ratio (\( W_1 \)) of air in an adiabatic saturation process, where air is saturated adiabatically to determine psychrometric properties.

Purpose: It is used in HVAC systems to analyze the psychrometric state of air, aiding in the design of humidification and cooling processes.

2. How Does the Calculator Work?

The calculator uses the following formula to calculate the entering humidity ratio:

Entering Humidity Ratio: \[ W_1 = \frac{(1093 - 0.556 T^*) W_2^* - 0.240 (T_1 - T^*)}{1093 + 0.444 T_1 - T^*} \]

Leaving Humidity Ratio (\( W_2^* \)) Calculation (if not provided): \[ W_2^* = 0.6219 \frac{P_s}{P - P_s} \] \[ P_s = 0.61078 \exp\left(\frac{17.27 T^*}{T^* + 237.3}\right) \, \text{(kPa, where \( T^* \) is in °C)} \]

Where:

  • \( W_1 \): Entering humidity ratio (lb_v/lb_da or kg_v/kg_da)
  • \( W_2^* \): Leaving humidity ratio (saturation at \( T^* \)) (lb_v/lb_da or kg_v/kg_da)
  • \( T_1 \): Entering air dry-bulb temperature (°F, °C, K)
  • \( T^* \): Thermodynamic wet-bulb temperature (°F, °C, K)
  • \( P \): Total pressure (psia, inHg, Pa)
  • \( P_s \): Saturation pressure at \( T^* \) (psia, inHg, Pa)
  • Constants: 1093 and 0.556 are approximate values based on vapor enthalpy and specific heat; 0.240 is the specific heat of dry air (\( C_{pa} \))

Unit Conversions:

  • Temperatures (\( T_1 \), \( T^* \)): °F, °C (°F = °C × 9/5 + 32), K (°F = (K - 273.15) × 9/5 + 32)
  • Pressure (\( P \)): psia, inHg (1 inHg = 0.491154 psia), Pa (1 Pa = 0.000145038 psia)
  • Humidity Ratios (\( W_1 \), \( W_2^* \)): lb_v/lb_da, kg_v/kg_da (numerically the same, label changes for clarity)

Steps:

  • Enter the entering dry-bulb temperature (\( T_1 \)) and thermodynamic wet-bulb temperature (\( T^* \)), and select their units.
  • Indicate whether you have \( W_2^* \) from Table 2-4 or need to calculate it.
  • If calculating \( W_2^* \), enter the total pressure (\( P \)); otherwise, input \( W_2^* \) directly.
  • Convert temperatures to °F and pressures to psia.
  • If calculating \( W_2^* \), compute the saturation pressure (\( P_s \)) at \( T^* \) using the Magnus-Tetens formula, then calculate \( W_2^* \).
  • Calculate the entering humidity ratio (\( W_1 \)) using the formula.
  • Display the result with 6 decimal places.

3. Importance of Adiabatic Saturation Process Calculation

Calculating the entering humidity ratio in an adiabatic saturation process is crucial for:

  • HVAC Design: Determines the psychrometric state of air, aiding in the design of humidification, cooling, and air conditioning systems.
  • Comfort and Health: Ensures appropriate humidity levels for occupant comfort and indoor air quality.
  • System Performance: Enables accurate calculations for psychrometric processes in HVAC systems.

4. Using the Calculator

Examples:

  • Example 1 (Using \( W_2^* \) from Table 2-4): For \( T_1 = 70^\circ \text{F} \), \( T^* = 60^\circ \text{F} \), \( W_2^* = 0.01104 \), result in lb_v/lb_da:
    • Numerator: \( (1093 - 0.556 \times 60) \times 0.01104 - 0.240 \times (70 - 60) \)
    • \( = (1093 - 33.36) \times 0.01104 - 0.240 \times 10 \)
    • \( = 1059.64 \times 0.01104 - 2.4 \approx 11.6984 - 2.4 = 9.2984 \)
    • Denominator: \( 1093 + 0.444 \times 70 - 60 \)
    • \( = 1093 + 31.08 - 60 = 1064.08 \)
    • \( W_1 = \frac{9.2984}{1064.08} \approx 0.008738 \)
  • Example 2 (Calculating \( W_2^* \)): For \( T_1 = 25^\circ \text{C} \), \( T^* = 15^\circ \text{C} \), \( P = 101325 \, \text{Pa} \), result in kg_v/kg_da:
    • Convert: \( T_1 = (25 \times 9/5) + 32 = 77^\circ \text{F} \), \( T^* = (15 \times 9/5) + 32 = 59^\circ \text{F} \), \( P = 101325 \times 0.000145038 = 14.6956 \, \text{psia} \)
    • Calculate \( P_s \): \( T^* = 15^\circ \text{C} \), \( P_s = 0.61078 \times \exp\left(\frac{17.27 \times 15}{15 + 237.3}\right) \approx 0.61078 \times \exp(1.0272) \approx 1.7058 \, \text{kPa} \), \( P_s = 1.7058 \times 0.145038 \approx 0.2474 \, \text{psia} \)
    • \( W_2^* = 0.6219 \times \frac{0.2474}{14.6956 - 0.2474} \approx 0.6219 \times \frac{0.2474}{14.4482} \approx 0.010645 \)
    • Numerator: \( (1093 - 0.556 \times 59) \times 0.010645 - 0.240 \times (77 - 59) \)
    • \( = (1093 - 32.804) \times 0.010645 - 0.240 \times 18 \)
    • \( = 1060.196 \times 0.010645 - 4.32 \approx 11.2863 - 4.32 = 6.9663 \)
    • Denominator: \( 1093 + 0.444 \times 77 - 59 \)
    • \( = 1093 + 34.188 - 59 = 1068.188 \)
    • \( W_1 = \frac{6.9663}{1068.188} \approx 0.006522 \)

5. Frequently Asked Questions (FAQ)

Q: What is an adiabatic saturation process?
A: An adiabatic saturation process is a psychrometric process where air is saturated with water vapor adiabatically (without heat exchange with the surroundings), reaching a saturation state at the thermodynamic wet-bulb temperature.

Q: Why is this calculation important in HVAC systems?
A: It helps determine the psychrometric properties of air, such as humidity ratio, which are essential for designing humidification, cooling, and air conditioning systems.

Q: How do I determine the leaving humidity ratio (\( W_2^* \)) if I don’t have Table 2-4?
A: The calculator computes \( W_2^* \) using the saturation pressure (\( P_s \)) at the thermodynamic wet-bulb temperature and total pressure, with \( P_s \) estimated via the Magnus-Tetens formula.

Adiabatic Saturation Process (Humidity Ratio) Calculator© - All Rights Reserved 2025