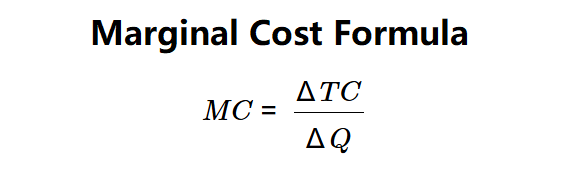Marginal Cost Calculator

1. What is the Marginal Cost Calculator?

Definition: This calculator computes the marginal cost ($ MC $), which represents the additional cost incurred by producing one more unit of a good or service.

Purpose: Helps businesses determine the cost efficiency of increasing production, aiding in pricing, production planning, and profit optimization.

2. How Does the Calculator Work?

The calculator follows a single-step process to compute $ MC $:

Formula:

$$ MC = \frac{\Delta TC}{\Delta Q} $$

Where:

$ MC $: Marginal Cost (dollars per unit)
$ \Delta TC $: Change in Total Cost (dollars)
$ \Delta Q $: Change in Quantity (units)

Steps:

Step 1: Determine $ TC1 $ and $ Q1 $. Input the total cost and quantity for the initial production level.
Step 2: Determine $ TC2 $ and $ Q2 $. Input the total cost and quantity for the increased production level (where $ Q2 > Q1 $).
Step 3: Calculate $ \Delta TC $. Subtract $ TC1 $ from $ TC2 $.
Step 4: Calculate $ \Delta Q $. Subtract $ Q1 $ from $ Q2 $.
Step 5: Calculate $ MC $. Divide $ \Delta TC $ by $ \Delta Q $.

3. Importance of Marginal Cost Calculation

Calculating $ MC $ is crucial for:

Production Decisions: Helps determine if producing additional units is cost-effective.
Pricing Strategy: Assists in setting prices to cover marginal costs and maximize profit.
Economic Analysis: Supports understanding of economies of scale and cost behavior.

4. Using the Calculator

Example 1 (Chairs): $ TC1 = \$5,000 $, $ Q1 = 10,000 $, $ TC2 = \$5,500 $, $ Q2 = 12,000 $:

Step 1: $ TC1 = \$5,000 $, $ Q1 = 10,000 $.
Step 2: $ TC2 = \$5,500 $, $ Q2 = 12,000 $.
Step 3: $ \Delta TC = 5,500 - 5,000 = \$500 $.
Step 4: $ \Delta Q = 12,000 - 10,000 = 2,000 $.
Step 5: $ MC = \frac{500}{2,000} = \$0.25 $ per unit.
Result: $ MC = \$0.25 $ per unit.

A marginal cost of $0.25 per chair suggests cost efficiency for the additional 2,000 units.

Example 2: $ TC1 = \$2,000 $, $ Q1 = 5,000 $, $ TC2 = \$2,300 $, $ Q2 = 6,000 $:

Step 1: $ TC1 = \$2,000 $, $ Q1 = 5,000 $.
Step 2: $ TC2 = \$2,300 $, $ Q2 = 6,000 $.
Step 3: $ \Delta TC = 2,300 - 2,000 = \$300 $.
Step 4: $ \Delta Q = 6,000 - 5,000 = 1,000 $.
Step 5: $ MC = \frac{300}{1,000} = \$0.30 $ per unit.
Result: $ MC = \$0.30 $ per unit.

A marginal cost of $0.30 per unit indicates a slight increase in cost efficiency.

Example 3: $ TC1 = \$1,000 $, $ Q1 = 2,000 $, $ TC2 = \$1,300 $, $ Q2 = 2,500 $:

Step 1: $ TC1 = \$1,000 $, $ Q1 = 2,000 $.
Step 2: $ TC2 = \$1,300 $, $ Q2 = 2,500 $.
Step 3: $ \Delta TC = 1,300 - 1,000 = \$300 $.
Step 4: $ \Delta Q = 2,500 - 2,000 = 500 $.
Step 5: $ MC = \frac{300}{500} = \$0.60 $ per unit.
Result: $ MC = \$0.60 $ per unit.

A marginal cost of $0.60 per unit reflects a higher incremental cost for additional production.

5. Frequently Asked Questions (FAQ)

Q: What is marginal cost?
A: Marginal cost ($ MC $) is the additional cost of producing one more unit of a good or service.

Q: Why might marginal cost decrease?
A: A decreasing $ MC $ can indicate economies of scale, where fixed costs are spread over more units.

Q: Can marginal cost be negative?
A: No, $ MC $ is typically non-negative; a negative value would indicate an error in cost or quantity data.