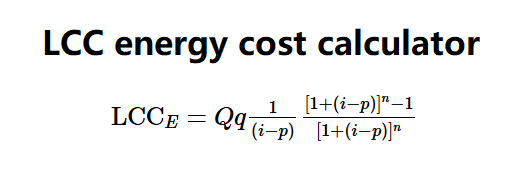How to Calculate LCC Energy Cost

The LCC Energy Cost Calculator computes the present value of future energy costs for energy-using devices and systems, accounting for escalating energy prices. The formula is:

Where:

• \( Q \): Yearly energy consumption.
• \( q \): Present energy price.
• \( p \): Expected annual rise of energy price (as a decimal).
• \( n \): Calculation period in years.
• \( i \): Interest rate (as a decimal).

Enter the values for Q, q, p, i, and n, and calculate the result.

Note: This formula uses an approximation suitable when rates are small. Ensure i > p and all values are positive.

Using the LCC Energy Cost Calculator

This calculator is useful for engineers and planners assessing the life-cycle costs of heat exchangers, filters, pipelines, and other plant items where energy costs escalate over time.

Input the yearly energy consumption (Q), present price (q), price rise rate (p), interest rate (i), and period (n). The calculator outputs the present value of future energy costs.

Example 1: For Q of 1000, q of 0.1, p of 0.03, i of 0.05, n of 10.

1. Q: 1000
2. q: 0.1
3. p: 0.03
4. i: 0.05
5. n: 10
6. Calculation: \( 1000 \times 0.1 \times \frac{1}{0.02} \times \frac{1.02^{10} - 1}{1.02^{10}} \approx 898.25000 \)
7. Result: 898.25000

Example 2: For Q of 500, q of 0.2, p of 0.02, i of 0.04, n of 5.

1. Q: 500
2. q: 0.2
3. p: 0.02
4. i: 0.04
5. n: 5
6. Calculation: \( 500 \times 0.2 \times \frac{1}{0.02} \times \frac{1.02^{5} - 1}{1.02^{5}} \approx 480.58000 \)
7. Result: 480.58000

Use this tool for quick life-cycle cost assessments in engineering projects.

Common FAQ

Below are frequently asked questions about LCC Energy Cost:

• Q: What is the LCC Energy Cost?
  A: It's the present value of future energy costs, accounting for price escalation and discounting.
• Q: What units should I use?
  A: Q in energy units/year (e.g., kWh/year), q in currency/unit (e.g., $/kWh), p and i as decimals (e.g., 0.05 for 5%), n in years.
• Q: Why use decimals for p and i?
  A: Rates are expressed as fractions in the formula (e.g., 5% = 0.05).
• Q: How accurate is this calculator?
  A: It provides precise results based on the approximation formula, rounded to 5 decimal places.
• Q: Can negative values be used?
  A: No, input values must be positive, and i must be greater than p; invalid inputs leave the result blank.

Advice on Interpreting Results

The calculated LCC_E represents the discounted total energy cost over the period, useful for comparing alternatives in life-cycle costing.

Note that this formula is an approximation of the exact growing annuity formula:

The approximation is valid when p and i are small (e.g., <10%). For more accuracy with higher rates, consider using the exact formula.

Keep in mind that this is one component of overall life-cycle cost analysis.