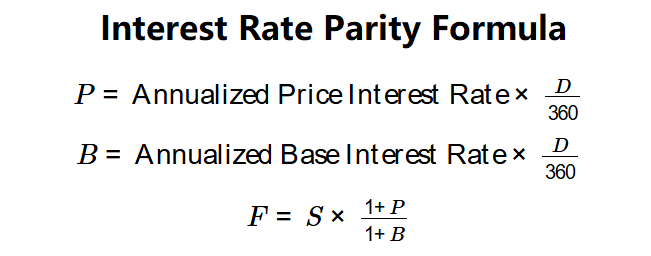Interest Rate Parity Calculator

1. What is the Interest Rate Parity Calculator?

Definition: The Interest Rate Parity Calculator computes the forward price of a currency pair (e.g., USD/EUR) using the covered interest rate parity model, adjusting for interest rate differentials.

Purpose: Helps traders and investors determine future exchange rates for hedging or speculation, ensuring no arbitrage opportunities.

2. How Does the Calculator Work?

The calculator evaluates the currency forward price in four steps using the following formulas:

Formulas:

\( P = \text{Annualized Price Interest Rate} \times \frac{D}{360} \)

\( B = \text{Annualized Base Interest Rate} \times \frac{D}{360} \)

\( F = S \times \frac{1 + P}{1 + B} \)

Where:

\( P \): Price currency interest rate (USD)
\( B \): Base currency interest rate (EUR)
\( F \): Currency forward price
\( S \): Spot price
\( D \): Number of days in the contract

Steps:

Step 1: Calculate Price Currency Interest Rate (\( P \)). Multiply the annualized USD interest rate by the fraction of the year (days/360).
Step 2: Calculate Base Currency Interest Rate (\( B \)). Multiply the annualized EUR interest rate by the fraction of the year (days/360).
Step 3: Get Current Spot Price (\( S \)). Input the current market exchange rate.
Step 4: Calculate Currency Forward Price (\( F \)). Multiply the spot price by the ratio of (1 + price currency interest rate) to (1 + base currency interest rate).

3. Importance of Interest Rate Parity Calculation

Calculating interest rate parity is crucial for:

Hedging: Protects against exchange rate risks in international trade.
Arbitrage Prevention: Ensures forward rates align with interest rate differentials.
Investment Strategy: Guides currency and interest rate investment decisions.

4. Using the Calculator

Example (USD/EUR): Days = 90, Annualized USD Interest Rate = 0.8%, Annualized EUR Interest Rate = 3.2%, Spot Price = 0.1735:

Step 1: \( P = 0.8\% \times \frac{90}{360} = 0.2\% \).
Step 2: \( B = 3.2\% \times \frac{90}{360} = 0.8\% \).
Step 3: Spot Price = 0.1735.
Step 4: \( F = 0.1735 \times \frac{1 + 0.002}{1 + 0.008} = 0.1725 \).
Results: Price Currency Interest Rate = 0.2%, Base Currency Interest Rate = 0.8%, Forward Price = 0.1725.

The forward price of 0.1725 indicates the expected USD/EUR exchange rate after 90 days.

5. Frequently Asked Questions (FAQ)

Q: What is covered interest rate parity?
A: Covered interest rate parity states that the forward exchange rate should incorporate interest rate differentials to prevent arbitrage.

Q: Why use 360 days?
A: The 360-day year is a convention in financial markets for simplicity in interest calculations.

Q: Can the forward price differ from the spot price?
A: Yes, it reflects the interest rate differential, as seen with 0.1725 < 0.1735 due to higher EUR rates.