Equivalent Interest Rate Calculator

Nominal Annual Interest Rate (\( r \)): %

Initial Compounding Frequency (\( m \)):

Desired Compounding Frequency (\( q \)):

1. What is Equivalent Interest Rate?

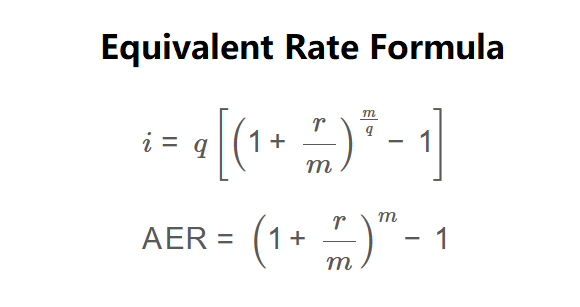
Definition: The Equivalent Interest Rate is the interest rate that would produce the same effective annual yield when compounded at a different frequency than the original rate.

Purpose: This calculation allows for comparison of interest rates with different compounding periods by converting them to equivalent rates with the same compounding frequency.

2. How Does the Equivalent Rate Calculator Work?

The calculator uses the following formula for Equivalent Interest Rate:

\[ i = q \left[ \left( 1 + \frac{r}{m} \right)^{\frac{m}{q}} - 1 \right] \]

For Effective Annual Rate (AER), the formula is:

\[ \text{AER} = \left( 1 + \frac{r}{m} \right)^m - 1 \]

Where:

\( r \): Nominal annual interest rate (in percentage)
\( m \): Initial compounding frequency (times per year)
\( q \): Desired compounding frequency (times per year)
\( i \): Equivalent interest rate (in percentage)

Steps:

Enter the Nominal Annual Interest Rate in percentage
Select the Initial Compounding Frequency
Select the Desired Compounding Frequency
The calculator converts the nominal rate to decimal form
Calculates the periodic rate (r/m)
Adjusts for the new compounding frequency (m/q)
Scales by the new compounding frequency (q)
Calculates AER using the initial compounding frequency
Converts back to percentage for display

3. Importance of Equivalent Rate Calculation

Calculating equivalent rates and AER is essential for:

Financial Product Comparison: Compare loans or investments with different compounding frequencies
Financial Planning: Understand the true cost or return when compounding changes
Loan Restructuring: Evaluate changes in payment schedules
Investment Analysis: Compare returns with different compounding periods

4. Using the Calculator

Example 1: Convert 8% compounded quarterly to an equivalent rate compounded monthly

Nominal Rate: 8%
Initial Compounding: Quarterly (4)
Desired Compounding: Monthly (12)
Equivalent Rate: \( i = 12 \left[ \left(1 + \frac{0.08}{4}\right)^{\frac{4}{12}} - 1 \right] ≈ 7.8698\% \)
AER: \( \text{AER} = \left(1 + \frac{0.08}{4}\right)^4 - 1 ≈ 8.2432\% \)

Example 2: Convert 5% compounded semi-annually to an equivalent rate compounded daily

Nominal Rate: 5%
Initial Compounding: Semi-annually (2)
Desired Compounding: Daily (365)
Equivalent Rate: \( i = 365 \left[ \left(1 + \frac{0.05}{2}\right)^{\frac{2}{365}} - 1 \right] ≈ 4.8793\% \)
AER: \( \text{AER} = \left(1 + \frac{0.05}{2}\right)^2 - 1 ≈ 5.0625\% \)

5. Frequently Asked Questions (FAQ)

Q: Why does the equivalent rate change with different compounding frequencies?
A: The rate adjusts to maintain the same effective annual yield despite the change in compounding frequency.

Q: When would I need to calculate equivalent rates?
A: When comparing financial products with different payment schedules or when changing the compounding frequency of an investment.

Q: Does more frequent compounding always result in a lower equivalent rate?
A: Yes, because the same effective yield can be achieved with a lower nominal rate when compounding more frequently.

Q: How is this different from effective annual rate?
A: EAR (or AER) converts to annual compounding, while equivalent rate can convert to any desired compounding frequency.