Economic Order Quantity Calculator

EOQ Calculator

1. What is the Economic Order Quantity Calculator?

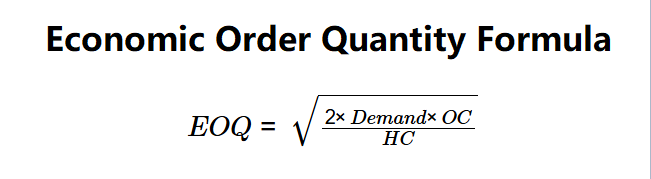
Definition: This calculator computes the economic order quantity ($ EOQ $), which determines the optimal order quantity that minimizes the total inventory costs (ordering and holding costs) for a given demand.

Purpose: Helps businesses optimize inventory management, reduce costs, and improve cash flow by determining the ideal order size.

2. How Does the Calculator Work?

The calculator uses the following formula to compute EOQ:

Formula:

$ EOQ = \sqrt{\frac{2 \times Demand \times OC}{HC}} $

Where:

$ EOQ $: Economic Order Quantity (units)
$ Demand $: Yearly Demand (units)
$ OC $: Order Cost (dollars)
$ HC $: Holding Cost (dollars per unit)

Steps:

Step 1: Determine $ Demand $. Input the total annual demand for the product.
Step 2: Determine $ OC $. Input the cost associated with placing an order.
Step 3: Determine $ HC $. Input the cost of holding one unit in inventory per year.
Step 4: Calculate $ EOQ $. Apply the formula to find the optimal order quantity.

Assumptions: Ordering and holding costs, as well as demand, remain constant throughout the year.

3. Importance of EOQ Calculation

Calculating EOQ is crucial for:

Cost Optimization: Minimizes the combined costs of ordering and holding inventory.
Inventory Management: Ensures efficient stock levels to avoid overstocking or stockouts.
Cash Flow Improvement: Reduces capital tied up in excess inventory.

4. Using the Calculator

Example 1 (Notepads): $ Demand = 500,000 $, $ OC = \$10 $, $ HC = \$4 $:

Step 1: $ Demand = 500,000 $ units.
Step 2: $ OC = \$10 $.
Step 3: $ HC = \$4 $ per unit.
Step 4: $ EOQ = \sqrt{\frac{2 \times 500,000 \times 10}{4}} = \sqrt{2,500,000} \approx 1,581.14 $ units.
Result: $ EOQ = 1,581.14 $ units.

An EOQ of 1,581.14 units optimizes inventory costs for notepads.

Example 2: $ Demand = 1,000,000 $, $ OC = \$15 $, $ HC = \$5 $:

Step 1: $ Demand = 1,000,000 $ units.
Step 2: $ OC = \$15 $.
Step 3: $ HC = \$5 $ per unit.
Step 4: $ EOQ = \sqrt{\frac{2 \times 1,000,000 \times 15}{5}} = \sqrt{6,000,000} \approx 2,449.49 $ units.
Result: $ EOQ = 2,449.49 $ units.

An EOQ of 2,449.49 units suggests a larger optimal order for higher demand.

Example 3: $ Demand = 250,000 $, $ OC = \$8 $, $ HC = \$2 $:

Step 1: $ Demand = 250,000 $ units.
Step 2: $ OC = \$8 $.
Step 3: $ HC = \$2 $ per unit.
Step 4: $ EOQ = \sqrt{\frac{2 \times 250,000 \times 8}{2}} = \sqrt{2,000,000} \approx 1,414.21 $ units.
Result: $ EOQ = 1,414.21 $ units.

An EOQ of 1,414.21 units indicates a moderate order size for lower demand.

5. Frequently Asked Questions (FAQ)

Q: What is economic order quantity?
A: Economic order quantity ($ EOQ $) is the optimal number of units to order that minimizes total inventory costs, balancing ordering and holding costs.

Q: What happens if holding costs increase?
A: An increase in holding costs reduces the $ EOQ $, leading to smaller, more frequent orders.

Q: Can EOQ be zero?
A: No, since demand, order cost, and holding cost are positive, $ EOQ $ will always be positive.