Effective Annual Rate (EAR) Calculator

1. What is the Effective Annual Rate (EAR)?

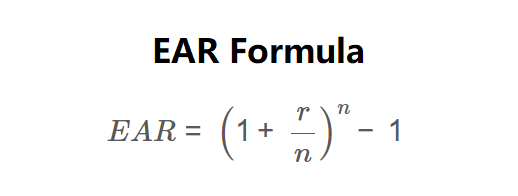
Definition: The Effective Annual Rate (EAR) is the actual interest rate that an investor earns or pays in a year after accounting for compounding.

Purpose: EAR provides a way to compare different investment or loan options with different compounding periods on a consistent basis.

2. How Does the EAR Calculator Work?

The calculator uses the following formula:

\[ EAR = \left(1 + \frac{r}{n}\right)^n - 1 \]

Where:

\( r \): Nominal annual interest rate (as a decimal)
\( n \): Number of compounding periods per year

Steps:

Enter the Nominal Interest Rate in percentage
Enter the number of Compounding Periods per Year
The calculator converts the nominal rate to decimal form
Calculates the periodic rate (r/n)
Applies the compounding effect ((1 + r/n)^n)
Subtracts 1 to get the EAR in decimal form
Converts back to percentage for display

3. Importance of EAR Calculation

Calculating EAR is essential for:

Investment Comparison: Compare investments with different compounding frequencies
Loan Evaluation: Understand the true cost of loans with different compounding periods
Financial Planning: Accurately project investment growth or loan costs

4. Using the Calculator

Example 1: Calculate EAR for a nominal rate of 8% compounded quarterly

Nominal Rate: 8%
Compounding Periods: 4
Calculation: \( EAR = \left(1 + \frac{0.08}{4}\right)^4 - 1 = 1.02^4 - 1 = 0.0824 \) or 8.24%

Example 2: Calculate EAR for a nominal rate of 5% compounded monthly

Nominal Rate: 5%
Compounding Periods: 12
Calculation: \( EAR = \left(1 + \frac{0.05}{12}\right)^{12} - 1 \approx 0.0512 \) or 5.12%

5. Frequently Asked Questions (FAQ)

Q: What's the difference between nominal rate and EAR?
A: Nominal rate doesn't account for compounding, while EAR shows the actual annual rate including compounding effects.

Q: Does more frequent compounding always mean higher EAR?
A: Yes, for a given nominal rate, more frequent compounding results in a higher EAR.

Q: What's the maximum possible EAR for a given nominal rate?
A: As compounding frequency approaches infinity, EAR approaches e^r - 1 (continuous compounding).