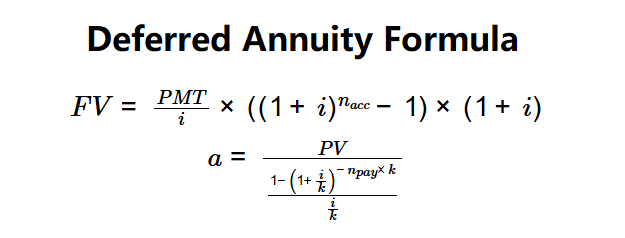Deferred Annuity Calculator

Regular Payment (PMT): $

Annual Interest Rate: %

Accumulation Phase Years: years

Payout Phase Years: years

Compounding Periods per Year (Payout Phase):

1. What is the Deferred Annuity Calculator?

Definition: The Deferred Annuity Calculator computes the future value of a series of regular payments during an accumulation phase and the regular withdrawal amount during a payout phase, accounting for interest and compounding.

Purpose: Helps retirees, investors, and financial planners estimate savings growth during the accumulation phase and sustainable withdrawals during the payout phase.

2. How Does the Calculator Work?

The calculator uses two formulas for the accumulation and payout phases:

Formulas:

$ FV = \frac{PMT}{i} \times \left( (1 + i)^{n_{acc}} - 1 \right) \times (1 + i) $

$ a = \frac{PV}{\frac{1 - \left(1 + \frac{i}{k}\right)^{-n_{pay} \times k}}{\frac{i}{k}}} $

Where:

$ FV $: Future value at end of accumulation phase ($)
$ PMT $: Regular payment during accumulation ($)
$ i $: Annual interest rate
$ n_{acc} $: Number of years in accumulation phase
$ a $: Regular withdrawal amount during payout ($ per period)
$ PV $: Present value at start of payout phase ($)
$ k $: Compounding periods per year in payout phase
$ n_{pay} $: Number of years in payout phase

Steps:

Step 1: Input Regular Payment. Enter the periodic payment during accumulation (e.g., $1000).
Step 2: Input Interest Rate. Enter the annual interest rate (e.g., 5%).
Step 3: Input Accumulation Years. Enter the number of years for accumulation (e.g., 10).
Step 4: Input Payout Years. Enter the number of years for withdrawals (e.g., 10).
Step 5: Select Compounding Periods. Choose monthly, quarterly, or annual compounding for the payout phase (e.g., monthly).
Step 6: Calculate. Compute the future value and regular withdrawal amount.

3. Importance of Deferred Annuity Calculation

Calculating deferred annuity values is crucial for:

Retirement Planning: Estimates savings growth and sustainable withdrawals for retirement.
Investment Analysis: Evaluates the value of deferred annuity products.
Financial Forecasting: Supports long-term budgeting for savings and income needs.

4. Using the Calculator

Example: Regular payment = $1000, Interest rate = 5%, Accumulation years = 10, Payout years = 10, Compounding = Monthly:

Step 1: $ PMT $ = $1000.
Step 2: $ i $ = 0.05.
Step 3: $ n_{acc} $ = 10.
Step 4: $ n_{pay} $ = 10.
Step 5: $ k $ = 12.
Step 6:
- $ FV = \frac{1000}{0.05} \times \left( (1 + 0.05)^{10} - 1 \right) \times (1 + 0.05) \approx 165,951.97 $.
- $ a = \frac{165,951.97}{\frac{1 - \left(1 + \frac{0.05}{12}\right)^{-10 \times 12}}{\frac{0.05}{12}}} \approx 1759.36 $.
Result: Future value = $165,951.97, Regular withdrawal = $1,759.36 per month.

This shows the savings at the end of accumulation and monthly withdrawals during payout.

5. Frequently Asked Questions (FAQ)

Q: What is a deferred annuity?
A: A deferred annuity involves an accumulation phase where payments are made and grow with interest, followed by a payout phase where withdrawals are received.

Q: Why does the payout phase use compounding periods?
A: Compounding periods determine how frequently interest is applied during withdrawals, affecting the withdrawal amount.

Q: Can the accumulation phase have zero years?
A: Yes, if accumulation years are zero, the future value is zero, and no withdrawals can be calculated.