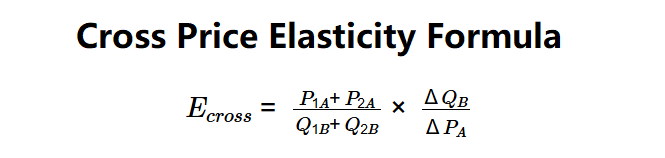Cross Price Elasticity Calculator

Cross-Price Elasticity Calculator

1. What is the Cross-Price Elasticity Calculator?

Definition: This calculator computes the cross-price elasticity of demand ($ E_{cross} $), which measures how the quantity demanded of one product (B) changes in response to a price change of another product (A), indicating whether they are substitutes or complements.

Purpose: Helps businesses and economists understand the relationship between two products, aiding in pricing strategies and market analysis.

2. How Does the Calculator Work?

The calculator uses the following formula to compute cross-price elasticity:

Formula:

$ E_{cross} = \frac{P_{1A} + P_{2A}}{Q_{1B} + Q_{2B}} \times \frac{\Delta Q_B}{\Delta P_A} $

Where:

$ E_{cross} $: Cross-Price Elasticity
$ P_{1A} $: Initial Price of Product A (dollars)
$ P_{2A} $: Final Price of Product A (dollars)
$ Q_{1B} $: Initial Quantity Sold of Product B (units)
$ Q_{2B} $: Final Quantity Sold of Product B (units)
$ \Delta Q_B $: Change in Quantity of Product B ($ Q_{2B} - Q_{1B} $)
$ \Delta P_A $: Change in Price of Product A ($ P_{2A} - P_{1A} $)

Steps:

Step 1: Determine $ P_{1A} $ and $ P_{2A} $. Identify the initial and final prices of Product A.
Step 2: Determine $ Q_{1B} $ and $ Q_{2B} $. Identify the initial and final quantities sold of Product B.
Step 3: Calculate $ E_{cross} $. Apply the formula using the average prices and quantities and their changes.

3. Importance of Cross-Price Elasticity Calculation

Calculating cross-price elasticity is crucial for:

Product Relationship Analysis: A positive $ E_{cross} $ indicates substitute goods; a negative value indicates complements.
Pricing Strategies: Helps businesses set prices to maximize demand or revenue.
Market Competition: Assists in understanding competitive dynamics between products.

4. Using the Calculator

Example 1 (Coca-Cola and Pepsi): $ P_{1A} = \$0.69 $, $ P_{2A} = \$0.59 $, $ Q_{1B} = 680,000,000 $, $ Q_{2B} = 600,000,000 $:

Step 1: $ P_{1A} = \$0.69 $, $ P_{2A} = \$0.59 $.
Step 2: $ Q_{1B} = 680,000,000 $, $ Q_{2B} = 600,000,000 $.
Step 3: $ E_{cross} = \frac{0.69 + 0.59}{680,000,000 + 600,000,000} \times \frac{600,000,000 - 680,000,000}{0.59 - 0.69} = \frac{1.28}{1,280,000,000} \times \frac{-80,000,000}{-0.10} \approx 0.80 $.
Result: $ E_{cross} = 0.80 $.

A positive elasticity of 0.80 indicates Coca-Cola and Pepsi are substitutes.

Example 2: $ P_{1A} = \$10 $, $ P_{2A} = \$12 $, $ Q_{1B} = 1000 $, $ Q_{2B} = 800 $:

Step 1: $ P_{1A} = \$10 $, $ P_{2A} = \$12 $.
Step 2: $ Q_{1B} = 1000 $, $ Q_{2B} = 800 $.
Step 3: $ E_{cross} = \frac{10 + 12}{1000 + 800} \times \frac{800 - 1000}{12 - 10} = \frac{22}{1800} \times \frac{-200}{2} \approx -1.22 $.
Result: $ E_{cross} = -1.22 $.

A negative elasticity of -1.22 indicates the products are complements.

Example 3: $ P_{1A} = \$5 $, $ P_{2A} = \$6 $, $ Q_{1B} = 5000 $, $ Q_{2B} = 5100 $:

Step 1: $ P_{1A} = \$5 $, $ P_{2A} = \$6 $.
Step 2: $ Q_{1B} = 5000 $, $ Q_{2B} = 5100 $.
Step 3: $ E_{cross} = \frac{5 + 6}{5000 + 5100} \times \frac{5100 - 5000}{6 - 5} = \frac{11}{10100} \times \frac{100}{1} \approx 0.11 $.
Result: $ E_{cross} = 0.11 $.

A positive elasticity of 0.11 suggests a weak substitute relationship.

5. Frequently Asked Questions (FAQ)

Q: What is cross-price elasticity?
A: Cross-price elasticity ($ E_{cross} $) measures how the quantity demanded of Product B changes when the price of Product A changes.

Q: What does a positive or negative elasticity mean?
A: Positive $ E_{cross} $ indicates substitutes (demand for B increases as A's price rises); negative indicates complements (demand for B decreases as A's price rises).

Q: Can cross-price elasticity be zero?
A: Yes, if the quantity demanded of Product B does not change with Product A's price, indicating no relationship.