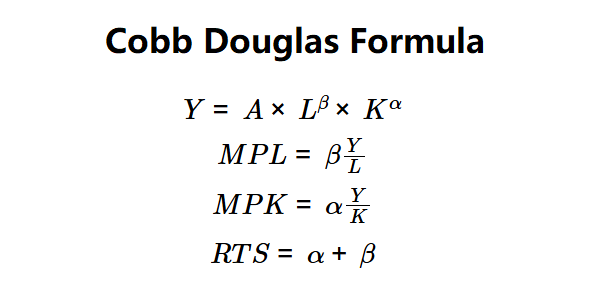Cobb Douglas Production Function Calculator

Total Factor Productivity (A):

Labor Input (L): units

Capital Input (K): units

Output Elasticity of Labor (β):

Output Elasticity of Capital (α):

Total Production (Y):

units

Marginal Product of Labor (MPL):

units per labor

Marginal Product of Capital (MPK):

units per capital

Returns to Scale (α + β):

1. What is the Cobb-Douglas Production Function Calculator?

Definition: The Cobb-Douglas Production Function Calculator computes the total production of a good based on labor and capital inputs, using the formula $ Y = A \times L^\beta \times K^\alpha $. It also calculates marginal products and returns to scale to analyze production efficiency.

Purpose: Helps businesses and economists understand how labor and capital contribute to output, optimize resource allocation, and assess production scalability.

2. How Does the Calculator Work?

The calculator uses the Cobb-Douglas production function to compute output and related metrics, following these steps and formulas:

Formulas:

$ Y = A \times L^\beta \times K^\alpha $

$ MPL = \beta \frac{Y}{L} $

$ MPK = \alpha \frac{Y}{K} $

$ RTS = \alpha + \beta $

Where:

$ Y $: Total production (units)
$ A $: Total factor productivity
$ L $: Labor input (units)
$ K $: Capital input (units)
$ \beta $: Output elasticity of labor (0 < β ≤ 1)
$ \alpha $: Output elasticity of capital (0 < α ≤ 1)
$ MPL $: Marginal product of labor (units per labor)
$ MPK $: Marginal product of capital (units per capital)
$ RTS $: Returns to scale (constant if = 1, increasing if > 1, decreasing if < 1)

Steps:

Step 1: Calculate Total Production ($ Y $). Multiply total factor productivity by labor and capital raised to their respective elasticities.
Step 2: Calculate Marginal Product of Labor ($ MPL $). Multiply $\beta$ by the ratio of total production to labor.
Step 3: Calculate Marginal Product of Capital ($ MPK $). Multiply $\alpha$ by the ratio of total production to capital.
Step 4: Calculate Returns to Scale ($ RTS $). Sum $\alpha$ and $\beta$ to determine if returns are constant, increasing, or decreasing.

3. Importance of Cobb-Douglas Production Function Calculation

Calculating the Cobb-Douglas production function is crucial for:

Economic Analysis: Understands how labor and capital drive output, aiding in productivity studies.
Business Decisions: Optimizes resource allocation to maximize production efficiency.
Policy Formulation: Informs policies to enhance economic growth through labor and capital productivity.

4. Using the Calculator

Example (Glass Ball Industry): $ A = 8 $, $ L = 30 $, $ K = 25 $, $ \beta = 0.4 $, $ \alpha = 0.6 $:

Step 1: $ Y = 8 \times 30^{0.4} \times 25^{0.6} = 215.13 $.
Step 2: $ MPL = 0.4 \times \frac{215.13}{30} = 2.87 $.
Step 3: $ MPK = 0.6 \times \frac{215.13}{25} = 5.16 $.
Step 4: $ RTS = 0.6 + 0.4 = 1 $ (Constant).
Results: $ Y = 215.13 $ units, $ MPL = 2.87 $ units per labor, $ MPK = 5.16 $ units per capital, $ RTS = 1 $ (Constant).

Using 30 workers and $25 of capital produces 215.13 glass balls, with constant returns to scale, meaning doubling inputs doubles output.

Example (Scaling Inputs): $ A = 8 $, $ L = 45 $, $ K = 30 $, $ \beta = 0.4 $, $ \alpha = 0.6 $:

Step 1: $ Y = 8 \times 45^{0.4} \times 30^{0.6} = 282.26 $.
Step 2: $ MPL = 0.4 \times \frac{282.26}{45} = 2.51 $.
Step 3: $ MPK = 0.6 \times \frac{282.26}{30} = 5.64 $.
Step 4: $ RTS = 0.6 + 0.4 = 1 $ (Constant).
Results: $ Y = 282.26 $ units, $ MPL = 2.51 $ units per labor, $ MPK = 5.64 $ units per capital, $ RTS = 1 $ (Constant).

Increasing labor to 45 and capital to $30 increases production to 282.26 glass balls, demonstrating constant returns.

5. Frequently Asked Questions (FAQ)

Q: What is the Cobb-Douglas production function?
A: It’s a mathematical model ($ Y = A \times L^\beta \times K^\alpha $) that describes how labor and capital inputs produce output, with constant or varying returns to scale.

Q: Why are output elasticities important?
A: They measure how responsive output is to changes in labor or capital, guiding resource allocation decisions.

Q: What does constant returns to scale mean?
A: When $\alpha + \beta = 1$, doubling inputs doubles output, indicating efficient scaling without diminishing or increasing returns.