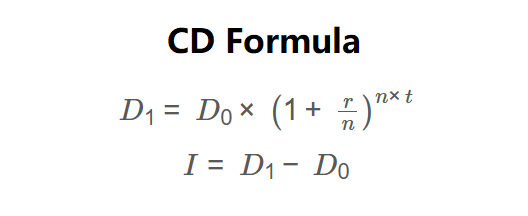Certificate of Deposit (CD) Calculator - Calculate Final Balance and Interest Earned

Initial Deposit ($ D_0 $):

Interest Rate ($ r $): %/year

Term ($ t $):

Compounding Frequency ($ n $):

1. What is the Certificate of Deposit (CD) Calculator?

Definition: This calculator computes the Final Balance ($ D_1 $) and Interest Earned ($ I $) for a Certificate of Deposit (CD) based on the Initial Deposit ($ D_0 $), Interest Rate ($ r $), Term ($ t $), and Compounding Frequency ($ n $). A CD is a savings product that earns interest over a fixed term.

Purpose: Savers and investors use this tool to estimate the growth of their money in a CD, helping to plan for future financial goals or compare CD options.

2. How Does the Calculator Work?

The calculator uses the following formulas, as shown in the image above:

$ D_1 = D_0 \times \left(1 + \frac{r}{n}\right)^{n \times t} $

$ I = D_1 - D_0 $

Where:

$ D_0 $: Initial Deposit (in selected currency);
$ r $: Annual Interest Rate (as a decimal, e.g., 5% = 0.05);
$ t $: Term (converted to years);
$ n $: Number of times interest is compounded per year;
$ D_1 $: Final Balance (in selected currency);
$ I $: Interest Earned (in selected currency).

Steps:

Enter the Initial Deposit ($ D_0 $) and select the currency (USD, EUR, GBP, JPY).
Enter the Interest Rate ($ r $) in percentage (e.g., 5 for 5%).
Enter the Term ($ t $) and select its unit (Daily, Monthly, Yearly).
Select the Compounding Frequency ($ n $) from the options: Annually (1), Quarterly (4), Monthly (12), or Daily (365).
The calculator converts the term to years, converts the interest rate to a decimal, computes the Final Balance, and then calculates the Interest Earned.
Results are formatted (scientific notation for values < 0.001, otherwise 4 decimal places) and displayed in the selected currency.

3. Importance of CD Calculation

Calculating the Final Balance and Interest Earned for a CD is essential for:

Financial Planning: Helps predict the future value of savings for budgeting or goal-setting.
Investment Comparison: Allows comparison of different CD options based on interest rates and terms.
Return Estimation: Provides a clear picture of earnings, aiding in decisions about locking money in a CD.

4. Using the Calculator

Example 1: Calculate the Final Balance and Interest Earned for a CD with an Initial Deposit of $10,000, an Interest Rate of 3%, a Term of 2 years, and monthly compounding, in USD:

Initial Deposit ($ D_0 $): $10,000;
Interest Rate ($ r $): 3% = 0.03;
Term ($ t $): 2 years;
Compounding Frequency ($ n $): Monthly = 12;
Final Balance ($ D_1 $): $ 10,000 \times \left(1 + \frac{0.03}{12}\right)^{12 \times 2} = 10,000 \times (1 + 0.0025)^{24} = 10,000 \times 1.0618 = 10,617.76 \, \text{USD} $;
Interest Earned ($ I $): $ 10,617.76 - 10,000 = 617.7600 \, \text{USD} $.

Example 2: Calculate the Final Balance and Interest Earned for a CD with an Initial Deposit of €5,000, an Interest Rate of 2%, a Term of 36 months, and quarterly compounding, in EUR:

Initial Deposit ($ D_0 $): €5,000;
Interest Rate ($ r $): 2% = 0.02;
Term ($ t $): 36 months = $ 36 \div 12 = 3 $ years;
Compounding Frequency ($ n $): Quarterly = 4;
Final Balance ($ D_1 $): $ 5,000 \times \left(1 + \frac{0.02}{4}\right)^{4 \times 3} = 5,000 \times (1 + 0.005)^{12} = 5,000 \times 1.0617 = 5,308.54 \, \text{EUR} $;
Interest Earned ($ I $): $ 5,308.54 - 5,000 = 308.5400 \, \text{EUR} $.

5. Frequently Asked Questions (FAQ)

Q: What happens if I withdraw my CD early?
A: This calculator assumes the CD is held to maturity. Early withdrawal may incur penalties, reducing the final balance and interest earned.

Q: Why does compounding frequency matter?
A: More frequent compounding increases the effective interest rate, leading to higher returns over the same term.

Q: Can the interest rate be negative?
A: While rare, negative interest rates can occur in certain economic conditions. The calculator allows this, but it’s not typical for CDs.