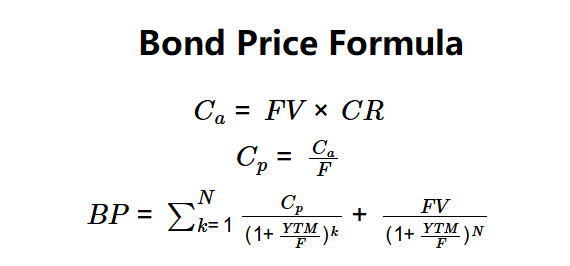Bond Price Calculator

Face Value: dollars

Annual Coupon Rate: %

Coupon Frequency:

Years to Maturity: years

Yield to Maturity (YTM): %

1. What is the Bond Price Calculator?

Definition: This calculator computes the bond price ($ BP $), coupon payment per period ($ C_p $), and annual coupon ($ C_a $), representing the present value of a bond’s cash flows based on its coupon payments and face value, discounted at the yield to maturity.

Purpose: Helps investors determine the fair market value of a bond, assess its attractiveness, and understand its cash flow structure for investment decisions.

2. How Does the Calculator Work?

The calculator follows a five-step process to compute the results:

Formulas:

$ C_a = FV \times CR $

$ C_p = \frac{C_a}{F} $

$ BP = \sum_{k=1}^{N} \frac{C_p}{(1 + \frac{YTM}{F})^k} + \frac{FV}{(1 + \frac{YTM}{F})^N} $

Where:

$ BP $: Bond Price (dollars)
$ C_p $: Coupon Payment per Period (dollars)
$ C_a $: Annual Coupon (dollars)
$ FV $: Face Value (dollars)
$ CR $: Annual Coupon Rate (decimal)
$ F $: Coupon Frequency (per year)
$ YTM $: Yield to Maturity (decimal)
$ N $: Total Periods ($ Years \times F $)

Steps:

Step 1: Determine face value. Use the bond’s principal amount at maturity ($ FV $).
Step 2: Calculate coupon per period. Compute $ C_a = FV \times CR $ and $ C_p = \frac{C_a}{F} $.
Step 3: Determine years to maturity. Use the number of years until the bond matures.
Step 4: Determine YTM. Use the annual rate of return if held to maturity.
Step 5: Calculate bond price. Sum the present value of all coupon payments and the face value, discounted at YTM.

3. Importance of Bond Price Calculation

Calculating the bond price and related metrics is crucial for:

Valuation: $ BP $ reflects the bond’s current market value, aiding in buy/sell decisions.
Cash Flow Analysis: $ C_p $ and $ C_a $ clarify periodic and annual income streams, essential for planning.
Yield Sensitivity: Helps investors understand how YTM impacts bond pricing.

4. Using the Calculator

Example (Bond A): $ FV = \$1,000 $, $ CR = 5\% $, $ F = 1 $, Years = 10, $ YTM = 8\% $:

Step 1: $ FV = \$1,000 $.
Step 2:
- $ C_a = 1,000 \times 0.05 = \$50 $.
- $ C_p = \frac{50}{1} = \$50 $.
Step 3: Years = 10.
Step 4: $ YTM = 8\% $.
Step 5: $ BP = \sum_{k=1}^{10} \frac{50}{(1 + 0.08)^k} + \frac{1,000}{(1 + 0.08)^{10}} = \$798.70 $.
Results: $ C_p = \$50 $, $ C_a = \$50 $, $ BP = \$798.70 $.

A bond price of $798.70 indicates the bond is trading at a discount due to a YTM higher than the coupon rate.

Example 2: $ FV = \$1,000 $, $ CR = 6\% $, $ F = 2 $, Years = 5, $ YTM = 7\% $:

Step 1: $ FV = \$1,000 $.
Step 2:
- $ C_a = 1,000 \times 0.06 = \$60 $.
- $ C_p = \frac{60}{2} = \$30 $.
Step 3: Years = 5.
Step 4: $ YTM = 7\% $.
Step 5: $ BP = \sum_{k=1}^{10} \frac{30}{(1 + \frac{0.07}{2})^k} + \frac{1,000}{(1 + \frac{0.07}{2})^{10}} = \$958.42 $.
Results: $ C_p = \$30 $, $ C_a = \$60 $, $ BP = \$958.42 $.

A bond price of $958.42 reflects a slight discount due to semi-annual coupons and a YTM above the coupon rate.

Example 3: $ FV = \$1,000 $, $ CR = 4\% $, $ F = 1 $, Years = 15, $ YTM = 3\% $:

Step 1: $ FV = \$1,000 $.
Step 2:
- $ C_a = 1,000 \times 0.04 = \$40 $.
- $ C_p = \frac{40}{1} = \$40 $.
Step 3: Years = 15.
Step 4: $ YTM = 3\% $.
Step 5: $ BP = \sum_{k=1}^{15} \frac{40}{(1 + 0.03)^k} + \frac{1,000}{(1 + 0.03)^{15}} = \$1,103.48 $.
Results: $ C_p = \$40 $, $ C_a = \$40 $, $ BP = \$1,103.48 $.

A bond price of $1,103.48 indicates a premium due to a YTM below the coupon rate.

5. Frequently Asked Questions (FAQ)

Q: Why is the bond price different from the face value?
A: $ BP $ varies from $ FV $ based on the relationship between $ YTM $ and $ CR $. If YTM > CR, the bond trades at a discount.

Q: Why include coupon per period and annual coupon?
A: $ C_p $ and $ C_a $ clarify the bond’s periodic and annual cash flows, essential for income planning, especially with non-annual frequencies.

Q: Can the bond price be negative?
A: No, since cash flows ($ C_p $, $ FV $) and discount rates are positive or zero, $ BP $ is always non-negative.