Bond Coupon Rate Calculator

1. What is the Bond Coupon Rate Calculator?

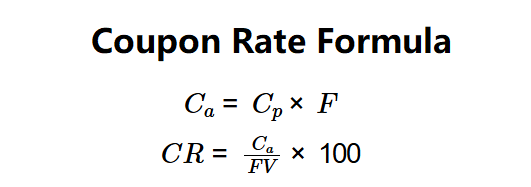
Definition: This calculator computes the annual coupon payment ($ C_a $) and coupon rate ($ CR $), representing the total yearly interest paid by a bond and the annual interest rate relative to its face value.

Purpose: Helps investors determine a bond’s fixed interest rate and income stream, aiding in bond evaluation and comparison.

2. How Does the Calculator Work?

The calculator follows a three-step process to compute the results:

Formulas:

$ C_a = C_p \times F $

$ CR = \frac{C_a}{FV} \times 100 $

Where:

$ C_a $: Annual Coupon Payment (dollars)
$ CR $: Coupon Rate (%)
$ C_p $: Coupon Payment per Period (dollars)
$ F $: Coupon Frequency (per year)
$ FV $: Face Value of Bond (dollars)

Steps:

Step 1: Determine face value. Use the bond’s principal at maturity ($ FV $).
Step 2: Calculate annual coupon payment. Compute $ C_a = C_p \times F $.
Step 3: Calculate coupon rate. Compute $ CR = \frac{C_a}{FV} \times 100 $.

3. Importance of Coupon Rate Calculation

Calculating the coupon rate and annual coupon payment is crucial for:

Income Assessment: $ C_a $ quantifies the yearly interest income, and $ CR $ indicates the bond’s fixed return relative to face value.
Bond Comparison: Allows investors to compare bonds with different face values and payment structures.
Investment Decisions: Helps evaluate a bond’s attractiveness based on its interest rate.

4. Using the Calculator

Example (Bond A): $ FV = \$1,000 $, $ C_p = \$25 $, $ F = 2 $:

Step 1: $ FV = \$1,000 $.
Step 2: $ C_a = 25 \times 2 = \$50 $.
Step 3: $ CR = \frac{50}{1,000} \times 100 = 5\% $.
Results: $ C_a = \$50 $, $ CR = 5\% $.

A coupon rate of 5% indicates the bond pays 5% of its face value annually as interest.

Example 2: $ FV = \$1,000 $, $ C_p = \$40 $, $ F = 1 $:

Step 1: $ FV = \$1,000 $.
Step 2: $ C_a = 40 \times 1 = \$40 $.
Step 3: $ CR = \frac{40}{1,000} \times 100 = 4\% $.
Results: $ C_a = \$40 $, $ CR = 4\% $.

A coupon rate of 4% reflects an annual interest payment of $40.

Example 3: $ FV = \$2,000 $, $ C_p = \$30 $, $ F = 4 $:

Step 1: $ FV = \$2,000 $.
Step 2: $ C_a = 30 \times 4 = \$120 $.
Step 3: $ CR = \frac{120}{2,000} \times 100 = 6\% $.
Results: $ C_a = \$120 $, $ CR = 6\% $.

A coupon rate of 6% indicates quarterly payments totaling $120 annually.

5. Frequently Asked Questions (FAQ)

Q: What is the coupon rate?
A: The coupon rate ($ CR $) is the annual interest rate paid by a bond, expressed as a percentage of its face value.

Q: How does frequency affect the coupon rate?
A: The coupon rate ($ CR $) is independent of frequency ($ F $), but frequency determines how the annual coupon ($ C_a $) is split into periodic payments ($ C_p $).

Q: Can the coupon rate be negative?
A: No, since $ C_a $ and $ FV $ are typically positive or non-negative, $ CR $ is non-negative.