Actual Cash Value Calculator

1. What is the Actual Cash Value Calculator?

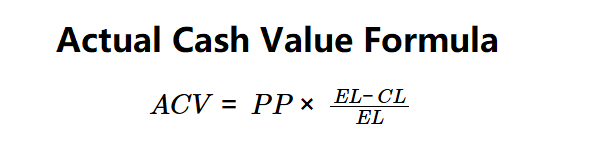
Definition: This calculator computes the actual cash value ($ ACV $) of a car, which represents its current value after accounting for depreciation based on its age and expected lifespan.

Purpose: Helps car owners, insurers, and buyers determine a vehicle's fair market value, useful for insurance claims, sales, or asset valuation.

2. How Does the Calculator Work?

The calculator follows a four-step process to compute the actual cash value:

Formula:

$ ACV = PP \times \frac{EL - CL}{EL} $

Where:

$ ACV $: Actual Cash Value (dollars)
$ PP $: Purchase Price (dollars)
$ EL $: Expected Life (years)
$ CL $: Current Life (years)

Steps:

Step 1: Determine $ PP $. Identify the original purchase price of the car.
Step 2: Estimate $ EL $. Determine the expected lifespan of the car in years.
Step 3: Calculate $ CL $. Determine the number of years the car has been used.
Step 4: Calculate $ ACV $. Apply the formula $ ACV = PP \times \frac{EL - CL}{EL} $.

3. Importance of Actual Cash Value Calculation

Calculating the actual cash value is crucial for:

Insurance Claims: Determines the payout for a totaled or stolen vehicle.
Asset Valuation: Helps assess the current worth of a car for financial reporting or resale.
Decision-Making: Aids in deciding whether to repair, sell, or replace a vehicle.

4. Using the Calculator

Example 1: $ PP = \$250,000 $, $ EL = 10 $, $ CL = 3 $:

Step 1: $ PP = \$250,000 $.
Step 2: $ EL = 10 $ years.
Step 3: $ CL = 3 $ years.
Step 4: $ ACV = 250,000 \times \frac{10 - 3}{10} = \$175,000 $.
Result: $ ACV = \$175,000 $.

An ACV of $175,000 indicates the car's current value after 3 years of use.

Example 2: $ PP = \$100,000 $, $ EL = 8 $, $ CL = 2 $:

Step 1: $ PP = \$100,000 $.
Step 2: $ EL = 8 $ years.
Step 3: $ CL = 2 $ years.
Step 4: $ ACV = 100,000 \times \frac{8 - 2}{8} = \$75,000 $.
Result: $ ACV = \$75,000 $.

An ACV of $75,000 reflects the car's value after 2 years.

Example 3: $ PP = \$50,000 $, $ EL = 5 $, $ CL = 4 $:

Step 1: $ PP = \$50,000 $.
Step 2: $ EL = 5 $ years.
Step 3: $ CL = 4 $ years.
Step 4: $ ACV = 50,000 \times \frac{5 - 4}{5} = \$10,000 $.
Result: $ ACV = \$10,000 $.

An ACV of $10,000 shows significant depreciation near the end of the car's expected life.

5. Frequently Asked Questions (FAQ)

Q: What is the actual cash value?
A: The actual cash value ($ ACV $) is the current market value of a car, calculated by adjusting its purchase price for depreciation based on its age and expected lifespan.

Q: How does the expected life affect the ACV?
A: A longer $ EL $ results in slower depreciation, increasing the $ ACV $, while a shorter $ EL $ accelerates depreciation, reducing the $ ACV $.

Q: Can the ACV be negative?
A: No, since $ PP $, $ EL $, and $ EL - CL $ are non-negative, the $ ACV $ is always non-negative.