1. What is the Power, Torque, RPM Calculator?

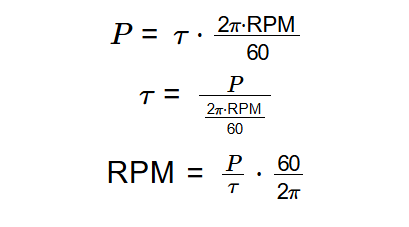
Definition: This calculator computes power, torque, or RPM using the formula \( P = \tau \cdot \frac{2\pi \cdot \text{RPM}}{60} \), relating power (watts), torque (Nm), and rotational speed (RPM).

Purpose: It assists engineers, automotive enthusiasts, and students in calculating engine or motor performance for vehicles, machinery, or mechanical systems.

2. How Does the Calculator Work?

The calculator uses the equations:

• \( P = \tau \cdot \frac{2\pi \cdot \text{RPM}}{60} \)
• \( \tau = \frac{P}{\frac{2\pi \cdot \text{RPM}}{60}} \)
• \( \text{RPM} = \frac{P}{\tau} \cdot \frac{60}{2\pi} \)

Where:

• \( P \): Power (in watts or HP);
• \( \tau \): Torque (in Nm or lb-ft);
• \( \text{RPM} \): Revolutions per minute;
• Results are displayed with 3 decimal places (or scientific notation if less than 0.001).

Steps:

• Select whether to calculate power, torque, or RPM.
• Enter the two required values (e.g., torque and RPM for power).
• Select appropriate units for inputs (if applicable).
• Click "Calculate" to compute the result.
• For power or torque, select the output unit (watts/HP or Nm/lb-ft).

3. Importance of Power, Torque, RPM Calculation

These calculations are crucial for:

• Engine Performance: Evaluating power output for vehicles or machinery.
• Mechanical Design: Ensuring motors and components meet performance requirements.
• Optimization: Tuning engines for efficiency or power in automotive applications.

4. Using the Calculator

Example 1: Calculate power for \( \tau = 100 \, \text{Nm} \), \( \text{RPM} = 3000 \), result in watts:

• Torque: 100 Nm;
• RPM: 3000;
• \( P = 100 \cdot \frac{2\pi \cdot 3000}{60} \approx 31415.926 \, \text{watts} \);
• Result: Power = 31415.926 watts.

Example 2: Calculate torque for \( P = 50 \, \text{HP} \), \( \text{RPM} = 2000 \), result in lb-ft:

• Power: 50 HP (37284.993579 watts);
• RPM: 2000;
• \( \tau = \frac{37284.993579}{\frac{2\pi \cdot 2000}{60}} \approx 177.653 \, \text{Nm} \);
• Convert to lb-ft: \( 177.653 \div 1.355817948 \approx 131.028 \, \text{lb-ft} \);
• Result: Torque = 131.028 lb-ft.

5. Frequently Asked Questions (FAQ)

Q: What is power in this context?
A: Power (\( P \)) is the rate of doing work, measured in watts or horsepower, indicating engine or motor output.

Q: What is torque?
A: Torque (\( \tau \)) is the rotational force produced by an engine, measured in Nm or lb-ft.

Q: What is RPM?
A: RPM (revolutions per minute) measures the rotational speed of an engine or motor shaft.

Q: Why must RPM be positive for power or torque calculations?
A: Positive RPM is required to avoid division by zero and ensure physically meaningful results.

Q: Why must torque be positive for RPM calculations?
A: Positive torque is needed to avoid division by zero and represent realistic engine output.

Q: How accurate is the formula?
A: The formula is exact for ideal conditions, with accuracy depending on the precision of input values.

Q: Can this calculator be used for electric motors?
A: Yes, it applies to any system where power, torque, and RPM are related, including electric motors.

Q: Why are results sometimes in scientific notation?
A: Results less than 0.001 are shown in scientific notation for readability, per the calculator’s formatting.

Q: What units can I use?
A: Torque: Nm, lb-ft; Power: watts, HP; RPM is unitless but entered as a number.

Q: How does this relate to vehicle performance?
A: Power and torque determine acceleration and speed, while RPM indicates engine operating speed.

Q: Can I use this for non-automotive applications?
A: Yes, it applies to any rotating machinery, such as turbines or industrial motors.

Q: What if I enter very high values?
A: High values are valid, but results may appear in scientific notation for readability.

Q: Does this account for losses?
A: No, the formula assumes ideal conditions; real-world losses (e.g., friction) require separate consideration.

Q: Is this calculator useful for tuning?
A: Yes, it helps estimate power or torque requirements for engine tuning or motor selection.

Q: Can I use this for educational purposes?
A: Yes, it’s ideal for students learning about rotational dynamics in engineering or physics.

RPM Power Torque Calculator© - All Rights Reserved 2025