Cm to Degrees Calculator

1. What is the Centimeters to Degrees Calculator?

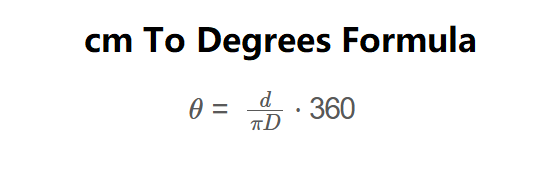
Definition: This calculator converts a distance along a circle's circumference (in centimeters or other units) to an angle in degrees, given the circle's diameter. It is used in contexts where angular measurements are needed based on linear distances, such as in engineering, physics, or geometry.

Purpose: It is used by engineers, scientists, and students to determine the angular displacement corresponding to a linear distance on a circular path, useful in applications like mechanical design, astronomy, or navigation.

2. How Does the Calculator Work?

The calculator uses the following formula, as shown in the image above:

\( \theta = \frac{d}{\pi D} \cdot 360 \)

Where:

\( \theta \): Angle (in degrees);
\( d \): Distance along the circumference (in centimeters);
\( D \): Diameter of the circle (in centimeters);
\( \pi \): Mathematical constant, approximately 3.14159.

Steps:

Enter the distance (\( d \)) and select its unit (centimeters, meters, inches, or feet).
Enter the diameter (\( D \)) and select its unit (centimeters, meters, inches, or feet).
The calculator converts both inputs to centimeters, computes the angle using the formula, and formats the result (scientific notation for values < 0.001, otherwise 4 decimal places).
Results are displayed for the angle, distance, and diameter.

3. Importance of Centimeters to Degrees Calculation

Calculating the angle from a linear distance is essential for:

Mechanical Design: Determines angular positions in rotating machinery, gears, or wheels based on linear measurements.
Astronomy and Navigation: Converts linear distances on celestial or terrestrial circles to angular measurements for positioning or tracking.
Education and Research: Supports learning and experimentation in geometry, trigonometry, and physics by relating linear and angular quantities.

4. Using the Calculator

Example 1: Calculate the angle for a distance of 50 cm along a circle with a diameter of 20 cm:

Distance (\( d \)): 50 cm;
Diameter (\( D \)): 20 cm;
Angle (\( \theta \)): \( \frac{50}{3.14159 \cdot 20} \cdot 360 = 286.4789 \text{ degrees} \).

Example 2: Calculate the angle for a distance of 1 meter along a circle with a diameter of 10 inches:

Distance (\( d \)): 1 m = 100 cm;
Diameter (\( D \)): 10 in = 25.4 cm;
Angle (\( \theta \)): \( \frac{100}{3.14159 \cdot 25.4} \cdot 360 = 451.3429 \text{ degrees} \).

5. Frequently Asked Questions (FAQ)

Q: How accurate is the centimeters to degrees calculation?
A: The formula is exact for circular arcs when inputs are accurate. The calculator uses π ≈ 3.14159 for precision, but real-world measurements may introduce errors.

Q: Why are multiple units offered for distance and diameter?
A: Different fields use different units (e.g., metric for science, imperial for engineering in some regions). Offering centimeters, meters, inches, and feet ensures versatility for global users.

Q: What happens if the angle exceeds 360 degrees?
A: Angles over 360 degrees indicate multiple rotations around the circle. The calculator provides the total angle, which can be reduced modulo 360 for a single rotation if needed.