Angular Velocity to RPM Calculator

1. What is the Angular Velocity to RPM Calculator?

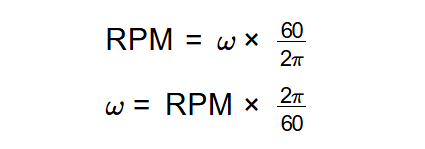
Definition: This calculator converts between angular velocity (\( \omega \)) in radians per second (rad/s) and revolutions per minute (RPM) using the formulas \( \text{RPM} = \omega \times \frac{60}{2\pi} \) and \( \omega = \text{RPM} \times \frac{2\pi}{60} \).

Purpose: It assists engineers, physicists, and students in converting rotational speed units for applications in mechanics, engineering, and physics.

2. How Does the Calculator Work?

The calculator uses the equations:

\( \text{RPM} = \omega \times \frac{60}{2\pi} \)
\( \omega = \text{RPM} \times \frac{2\pi}{60} \)

Where:

\( \omega \): Angular velocity in radians per second (rad/s);
\( \text{RPM} \): Revolutions per minute;
\( \pi \): Mathematical constant (approximately 3.14159);
Results are displayed with 3 decimal places (or scientific notation if less than 0.001).

Steps:

Select whether to convert from angular velocity to RPM or RPM to angular velocity.
Enter the value in the chosen unit (rad/s or RPM).
Click "Calculate" to compute the converted value.

3. Importance of Angular Velocity to RPM Conversion

Converting between angular velocity and RPM is crucial for:

Mechanical Engineering: Analyzing rotational systems like engines or turbines.
Physics Education: Understanding rotational motion concepts.
Automotive Applications: Relating engine speed to performance metrics.

4. Using the Calculator

Example 1: Convert an angular velocity of \( \omega = 100 \, \text{rad/s} \) to RPM:

Angular Velocity: 100 rad/s;
\( \text{RPM} = 100 \times \frac{60}{2 \times 3.14159} \approx 954.929 \, \text{RPM} \);
Result: RPM = 954.929.

Example 2: Convert an RPM of \( 1000 \, \text{RPM} \) to angular velocity:

RPM: 1000;
\( \omega = 1000 \times \frac{2 \times 3.14159}{60} \approx 104.719 \, \text{rad/s} \);
Result: Angular Velocity = 104.719 rad/s.

5. Frequently Asked Questions (FAQ)

Q: What is angular velocity?
A: Angular velocity (\( \omega \)) is the rate of rotation, measured in radians per second (rad/s).

Q: What is RPM?
A: RPM (revolutions per minute) measures the number of complete rotations per minute of a rotating object.

Q: Why convert between angular velocity and RPM?
A: Different fields use different units; angular velocity is common in physics, while RPM is used in engineering and automotive contexts.

Q: Why must the input value be non-negative?
A: Angular velocity and RPM represent rotational speeds, which are non-negative in realistic scenarios.

Q: How accurate is the conversion?
A: The conversion is exact, using the mathematical constant \( \pi \), with accuracy depending on input precision.

Q: What is the role of \( \pi \) in the formula?
A: \( \pi \) relates the angular displacement in radians to one full revolution (2\( \pi \) radians).

Q: Can this calculator be used for electric motors?
A: Yes, it applies to any rotating system, including electric motors, engines, or turbines.

Q: Why are results sometimes in scientific notation?
A: Results less than 0.001 are shown in scientific notation for readability, per the calculator’s formatting.

Q: Can I use this for non-mechanical applications?
A: Yes, it applies to any system with rotational motion, such as physics experiments or robotics.

Q: What if I enter a very high value?
A: High values are valid, but results may appear in scientific notation for readability.

Q: Does this account for real-world losses?
A: No, the formula assumes ideal conditions; real-world factors like friction require separate consideration.

Q: How does this relate to vehicle performance?
A: RPM is a key metric for engine speed, and converting to angular velocity helps analyze rotational dynamics.

Q: Can this be used for educational purposes?
A: Yes, it’s ideal for students learning about rotational motion in physics or engineering courses.

Q: Why is 60 used in the formula?
A: The factor 60 converts seconds to minutes, aligning angular velocity (rad/s) with RPM (revolutions per minute).

Q: Can I use this for planetary motion?
A: Yes, it can convert rotational speeds for celestial bodies if measured in rad/s or RPM.