 Home
Home
 Back
Back
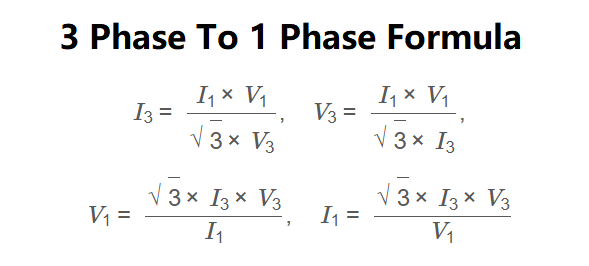
Error: Exactly three values must be provided!
Definition: This calculator computes the missing electrical parameter in a balanced system by converting values between three-phase and single-phase circuits using the formula \( \sqrt{3} \times I_3 \times V_3 = I_1 \times V_1 \).
Purpose: It is used in electrical engineering to relate currents and voltages between three-phase and single-phase systems, assuming a balanced three-phase setup.
The calculator uses the following formula:
Formula: \[ \sqrt{3} \times I_3 \times V_3 = I_1 \times V_1 \] Rearranged forms: \[ I_3 = \frac{I_1 \times V_1}{\sqrt{3} \times V_3}, \quad V_3 = \frac{I_1 \times V_1}{\sqrt{3} \times I_3}, \quad V_1 = \frac{\sqrt{3} \times I_3 \times V_3}{I_1}, \quad I_1 = \frac{\sqrt{3} \times I_3 \times V_3}{V_1} \] where:
Steps:
Calculating these conversions is crucial for:
Examples:
Q: What assumptions does this calculator make?
A: It assumes a balanced three-phase system with equal voltages and currents across phases.
Q: Why is √3 used in the formula?
A: √3 accounts for the 120-degree phase difference in three-phase systems.
Q: Can this be used for unbalanced systems?
A: No, for unbalanced systems, more detailed analysis is required.