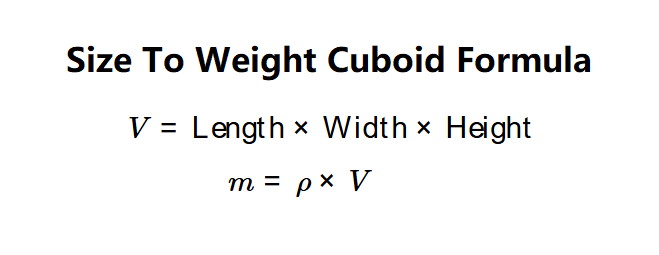Size to Weight Calculator (Rectangular Cuboid)

Length:

Width:

Height:

Density (\( \rho \)):

Volume (\( V \)):

Weight (\( m \)):

1. What is Size to Weight Calculator (Rectangular Cuboid)?

Definition: This calculator computes the volume and weight of a rectangular cuboid based on its dimensions (length, width, height) and the density of the material inside the cuboid.

Purpose: It helps users estimate the weight of a box or container without a scale, which is useful for shipping, storage, or material handling purposes.

2. How Does the Calculator Work?

The calculator uses the following equations to compute the volume and weight:

Volume: \( V = \text{Length} \times \text{Width} \times \text{Height} \)
Weight: \( m = \rho \times V \)

Where:

\( V \): Volume (in cubic meters or other units);
\( \text{Length}, \text{Width}, \text{Height} \): Dimensions of the cuboid;
\( \rho \): Density of the material;
\( m \): Mass or weight of the cuboid.

Steps:

Enter the length, width, and height of the cuboid, along with their units (feet, inches, yards, meters, centimeters, or millimeters).
Enter the density of the material and its unit (kg/m³, g/cm³, or lb/ft³).
Convert all dimensions to meters and density to kg/m³.
Calculate the volume in cubic meters: \( V = \text{Length} \times \text{Width} \times \text{Height} \).
Calculate the weight in kilograms: \( m = \rho \times V \).
Convert the volume and weight to the selected units.
Display results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Size to Weight Calculation

Calculating the weight of a cuboid is crucial for:

Shipping and Logistics: Estimating the weight of a package for shipping costs and handling requirements.
Material Handling: Determining the load on structures or equipment when storing or transporting heavy boxes.
Design and Engineering: Assessing the weight of components made of specific materials for design purposes.

4. Using the Calculator

Example 1 (Water-Filled Box): Calculate the volume and weight of a box filled with water:

Length: 1 m;
Width: 0.5 m;
Height: 0.2 m;
Density of water: 1000 kg/m³;
Volume: \( V = 1 \times 0.5 \times 0.2 = 0.1 \, \text{m}^3 \);
Weight: \( m = 1000 \times 0.1 = 100 \, \text{kg} \);
Volume in cubic feet: \( 0.1 \div 0.0283168 \approx 3.5315 \, \text{ft}^3 \);
Weight in pounds: \( 100 \times 2.20462 \approx 220.4620 \, \text{lb} \);
Result: \( V = 3.5315 \, \text{ft}^3 \), Weight = 220.4620 lb.

Example 2 (Steel Box): Calculate the volume and weight of a box made of steel:

Length: 50 cm;
Width: 30 cm;
Height: 20 cm;
Density of steel: 7.85 g/cm³;
Convert dimensions: Length = 0.5 m, Width = 0.3 m, Height = 0.2 m;
Volume: \( V = 0.5 \times 0.3 \times 0.2 = 0.03 \, \text{m}^3 \);
Convert density: \( 7.85 \times 1000 = 7850 \, \text{kg/m}^3 \);
Weight: \( m = 7850 \times 0.03 = 235.5 \, \text{kg} \);
Volume in cubic centimeters: \( 0.03 \times 1000000 = 30000 \, \text{cm}^3 \);
Weight in grams: \( 235.5 \times 1000 = 235500 \, \text{g} \);
Result: \( V = 30000 \, \text{cm}^3 \), Weight = 235500 g.

5. Frequently Asked Questions (FAQ)

Q: Why do I need to know the density of the material?
A: Density is required to calculate the weight of the cuboid, as it relates the volume to the mass using the formula \( m = \rho \times V \).

Q: How do I find the density of a material?
A: You can look up the density of common materials online or in reference books. For example, water has a density of 1000 kg/m³, and steel is approximately 7850 kg/m³.

Q: What happens if my units don’t match?
A: The calculator automatically converts all units to a consistent system (meters for volume, kg/m³ for density, kg for weight) before performing calculations, ensuring accurate results.