1. What is a Ramp Calculator?

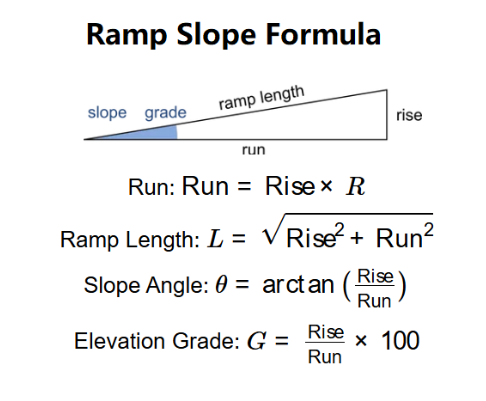
Definition: This calculator determines the **Rise**, **Run**, and **Ramp Length (L)** based on either the **Run** or **Rise** input, along with **Elevation Grade (G)** or **Slope Angle (θ)**, and provides the complementary value (Angle or Grade).

Purpose: It assists in designing ramps for accessibility, construction, or engineering projects by calculating key dimensions.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Rise: \[ Rise = Run \times \frac{G}{100} \quad \text{(if using Grade and Run is input)} \] \[ Rise = Run \times \tan(\theta) \quad \text{(if using Angle and Run is input)} \] \[ Run = \frac{Rise}{\frac{G}{100}} \quad \text{(if using Grade and Rise is input)} \] \[ Run = \frac{Rise}{\tan(\theta)} \quad \text{(if using Angle and Rise is input)} \] Ramp Length (L): \[ L = \sqrt{Rise^2 + Run^2} \] Complementary Calculation: \[ \theta = \arctan\left(\frac{Rise}{Run}\right) \quad \text{(converted to degrees if Grade is input)} \] \[ G = \tan(\theta) \times 100 \quad \text{(as a percentage if Angle is input)} \] Where:

• \(Run\): Horizontal distance along the ground (m)
• \(G\): Elevation Grade (as a percentage)
• \(\theta\): Slope Angle (in degrees, 0° to 90°)
• \(Rise\): Vertical height (m)
• \(L\): Ramp Length (m)

Unit Conversions:

• Length: m, ft (1 ft = 0.3048 m), cm (1 cm = 0.01 m), in (1 in = 0.0254 m), yd (1 yd = 0.9144 m)

Steps:

• Select whether to input Run or Rise
• Enter the chosen value (Run or Rise), selecting the unit (m, ft, cm, in, yd)
• Select input type (Grade % or Angle °) and enter the value
• Convert inputs to SI units (m)
• Calculate the other parameter (Rise or Run), Ramp Length, and the complementary value (Angle or Grade)
• Select desired units for each result and view converted values

3. Importance of Ramp Calculation

Calculating ramp dimensions is essential for:

• Accessibility: Ensuring ramps meet safety and regulatory standards (e.g., ADA guidelines).
• Design: Planning construction projects with appropriate slope and length.
• Safety: Preventing excessive slopes that could be hazardous.

4. Using the Calculator

Example 1 (Run): For a Run of 10 m and an Elevation Grade of 10%:

• Rise: \( Rise = 10 \times \frac{10}{100} = 1 \, \text{m} \)
• Run: \( 10 \, \text{m} \)
• Ramp Length: \( L = \sqrt{1^2 + 10^2} = \sqrt{101} \approx 10.050 \, \text{m} \)
• Slope Angle: \( \theta = \arctan\left(\frac{1}{10}\right) \approx 5.710 \, \text{°} \)

Example 2 (Rise): For a Rise of 1 m and a Slope Angle of 5.71°:

• Run: \( Run = \frac{1}{\tan(5.71°)} \approx 10 \, \text{m} \)
• Rise: \( 1 \, \text{m} \)
• Ramp Length: \( L = \sqrt{1^2 + 10^2} \approx 10.050 \, \text{m} \)
• Elevation Grade: \( G = \tan(5.71°) \times 100 \approx 10.000 \, \text{%} \)

5. Frequently Asked Questions (FAQ)

Q: What is Elevation Grade?
A: Elevation Grade (G) is the slope percentage, calculated as \( G = \frac{Rise}{Run} \times 100 \).

Q: What is Slope Angle?
A: Slope Angle (θ) is the angle of the ramp in degrees, where \( \tan(\theta) = \frac{Rise}{Run} \), and should be between 0° and 90°.

Q: Why is Ramp Length important?
A: It determines the total distance of the ramp, ensuring it fits the design space and meets safety standards.

Ramp Calculator© - All Rights Reserved 2025