K-Factor Calculator

Material Thickness (\( T \)):

Inner Radius (\( R_i \)):

Bend Angle (\( \theta \)) (degrees):

Bend Allowance (\( BA \)):

1. What is K-Factor Calculator?

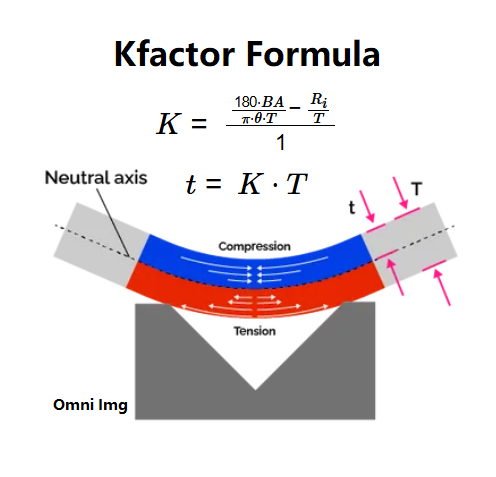
Definition: This calculator computes the K-factor for a metal sheet bending process, which indicates the position of the neutral axis, and the distance of the neutral axis from the inner surface (\( t \)).

Purpose: It assists users in sheet metal fabrication by determining the K-factor and neutral axis position, essential for accurate bend allowance calculations and flat pattern development.

2. How Does the Calculator Work?

The calculator uses the following equations:

\( K = \frac{\frac{180 \cdot BA}{\pi \cdot \theta \cdot T} - \frac{R_i}{T}}{1} \)
\( t = K \cdot T \)

Where:

\( K \): K-factor (dimensionless);
\( T \): Material thickness (converted to mm for calculation);
\( R_i \): Inner radius (converted to mm for calculation);
\( \theta \): Bend angle in degrees;
\( BA \): Bend allowance (converted to mm for calculation);
\( \pi \approx 3.14159 \);
\( t \): Distance of the neutral axis from the inner surface (converted to the selected output unit: mm, cm, m, in, ft).

Steps:

Enter the material thickness (\( T \)) and its unit (mm, cm, m, in, ft).
Enter the inner radius (\( R_i \)) and its unit.
Enter the bend angle (\( \theta \)) in degrees.
Enter the bend allowance (\( BA \)) and its unit.
Convert all measurements to millimeters.
Calculate the K-factor: \( K = \frac{\frac{180 \cdot BA}{\pi \cdot \theta \cdot T} - \frac{R_i}{T}}{1} \).
Calculate the neutral axis distance: \( t = K \cdot T \), in millimeters.
Convert the neutral axis distance to the selected output unit (mm, cm, m, in, ft).
Display results: K-factor and neutral axis distance, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of K-Factor Calculation

Calculating the K-factor is crucial for:

Accurate Fabrication: Ensures precise flat pattern development for sheet metal bending.
Material Efficiency: Minimizes material waste by accurately predicting bend allowances.
Design Precision: Helps engineers and fabricators achieve the desired dimensions after bending.

4. Using the Calculator

Example 1 (Omni Calculator Example): Calculate the K-factor for a metal sheet:

Material Thickness: 1 mm;
Inner Radius: 1 mm;
Bend Angle: 90°;
Bend Allowance: 2.1 mm;
K-Factor: \( K = \frac{\frac{180 \cdot 2.1}{\pi \cdot 90 \cdot 1} - \frac{1}{1}}{1} \);
\( K = \frac{\frac{378}{\pi \cdot 90} - 1}{1} \approx \frac{1.337 - 1}{1} = 0.337 \);
Neutral Axis Distance: \( t = 0.337 \times 1 = 0.337 \, \text{mm} \);
Convert to cm: \( t = 0.337 / 10 = 0.0337 \, \text{cm} \);
Result: K-Factor = 0.3370, Neutral Axis Distance = 0.0337 cm.

Example 2 (Different Units): Calculate the K-factor for a metal sheet:

Material Thickness: 0.1 in;
Inner Radius: 0.2 in;
Bend Angle: 45°;
Bend Allowance: 0.157 in;
Convert to mm: \( T = 0.1 \times 25.4 = 2.54 \, \text{mm} \), \( R_i = 0.2 \times 25.4 = 5.08 \, \text{mm} \), \( BA = 0.157 \times 25.4 = 3.9878 \, \text{mm} \);
K-Factor: \( K = \frac{\frac{180 \cdot 3.9878}{\pi \cdot 45 \cdot 2.54} - \frac{5.08}{2.54}}{1} \);
\( K = \frac{\frac{717.804}{\pi \cdot 45 \cdot 2.54} - 2}{1} \approx \frac{2 - 2}{1} = 0 \);
Neutral Axis Distance: \( t = 0 \times 2.54 = 0 \, \text{mm} \);
Convert to inches: \( t = 0 / 25.4 = 0 \, \text{in} \);
Result: K-Factor = 0.0000, Neutral Axis Distance = 0.0000 in.

5. Frequently Asked Questions (FAQ)

Q: What is the K-factor?
A: The K-factor is a ratio that represents the position of the neutral axis during sheet metal bending, typically between 0 and 1.

Q: Why is the neutral axis important?
A: The neutral axis is the layer within the material that neither stretches nor compresses during bending, crucial for calculating accurate bend allowances.

Q: Can this calculator handle complex bending scenarios?
A: This calculator assumes a single bend with constant thickness and radius. For complex bends, you may need to calculate each segment separately.