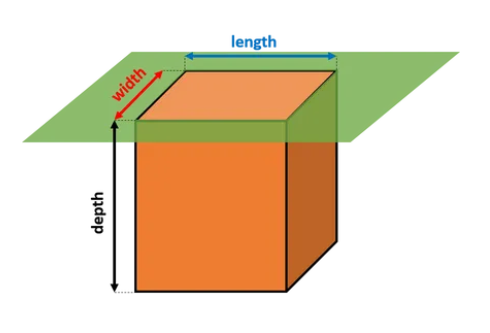
1. What is Cubic Yard Calculator?
Definition: This calculator computes the volume in cubic yards for various shapes, such as rectangular cuboids, cubes, cylinders, hollow cuboids, hollow cylinders, hemispheres, cones, and pyramids, based on user-provided dimensions. It also estimates the cost of materials based on the price per cubic yard.
Purpose: It assists contractors, landscapers, and homeowners in determining the amount of material (e.g., concrete, gravel, soil) needed for construction or landscaping projects and the associated costs, preventing over- or under-purchasing.
2. How Does the Calculator Work?
The calculator uses the following equations to compute volume based on the shape:
- Rectangular Cuboid: \( V = \text{Length} \times \text{Width} \times \text{Depth} \)
- Cube: \( V = \text{Length}^3 \)
- Cylinder: \( V = \pi \times \text{Radius}^2 \times \text{Depth} \)
- Hollow Cylinder: \( V = \pi \times (\text{Outer Radius}^2 - \text{Inner Radius}^2) \times \text{Depth} \)
- Hemisphere: \( V = \frac{2}{3} \pi \times \text{Radius}^3 \)
- Cone: \( V = \frac{1}{3} \pi \times \text{Radius}^2 \times \text{Depth} \)
- Pyramid: \( V = \frac{1}{3} \times \text{Base Area} \times \text{Depth} \)
- Convert to Cubic Yards: \( V_{\text{yd}^3} = \frac{V_{\text{ft}^3}}{27} \)
- Cost: \( \text{Cost} = V_{\text{yd}^3} \times \text{Price per yd}^3 \)
Where:
- \( V \): Volume;
- \( \text{Length}, \text{Width}, \text{Depth} \): Dimensions for rectangular cuboid, cube, or hollow cuboid;
- \( \text{Radius} \): Radius of cylinder, hollow cylinder, hemisphere, or cone;
- \( \text{Outer Radius}, \text{Inner Radius} \): Radii for hollow cylinder;
- \( \text{Base Area} \): Base area for pyramid;
- \( \pi \approx 3.14159 \).
Steps:
- Select the shape (rectangular cuboid, cube, cylinder, etc.).
- Enter the dimensions for the selected shape and their units (feet, inches, yards, meters, centimeters, millimeters).
- Enter the price per cubic yard for cost estimation.
- Convert all dimensions to feet (or square feet for area).
- Calculate the volume in cubic feet using the appropriate formula.
- Convert the volume to cubic yards (\( V_{\text{ft}^3} / 27 \)) or other selected units.
- Calculate the total cost by multiplying the volume in cubic yards by the price per cubic yard.
- Display results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.
3. Importance of Cubic Yard Calculation
Calculating cubic yards is essential for:
- Construction: Estimating the amount of concrete needed for slabs, footers, or columns.
- Landscaping: Determining the volume of mulch, soil, or gravel for gardens or driveways.
- Cost Management: Avoiding overspending by accurately calculating material requirements.
4. Using the Calculator
Example 1 (Rectangular Cuboid): Calculate the volume and cost for a concrete slab with the following inputs:
- Shape: Rectangular Cuboid;
- Length: 12 ft;
- Width: 10 ft;
- Depth: 6 in;
- Price per Cubic Yard: $100;
- Convert depth: \( 6 \, \text{in} = 6 / 12 = 0.5 \, \text{ft} \);
- Volume in cubic feet: \( V = 12 \times 10 \times 0.5 = 60 \, \text{ft}^3 \);
- Volume in cubic yards: \( V = 60 / 27 \approx 2.2222 \, \text{yd}^3 \);
- Cost: \( 2.2222 \times 100 = 222.22 \, \$ \);
- Result: \( V = 2.2222 \, \text{yd}^3 \), Cost = $222.22.
Example 2 (Hollow Cylinder): Calculate the volume and cost for a hollow cylindrical tank:
- Shape: Hollow Cylinder;
- Outer Radius: 6 ft;
- Inner Radius: 5 ft;
- Depth: 10 ft;
- Price per Cubic Yard: $50;
- Volume in cubic feet: \( V = \pi \times (6^2 - 5^2) \times 10 = \pi \times (36 - 25) \times 10 \approx 345.5752 \, \text{ft}^3 \);
- Volume in cubic yards: \( V = 345.5752 / 27 \approx 12.7991 \, \text{yd}^3 \);
- Cost: \( 12.7991 \times 50 \approx 639.95 \, \$ \);
- Result: \( V = 12.7991 \, \text{yd}^3 \), Cost = $639.95.
5. Frequently Asked Questions (FAQ)
Q: What is a cubic yard?
A: A cubic yard is a unit of volume equal to the volume of a cube with sides of 1 yard (3 feet), or 27 cubic feet.
Q: How do I convert cubic feet to cubic yards?
A: Divide the volume in cubic feet by 27 to get the volume in cubic yards.
Q: Why is depth important in volume calculations?
A: Depth determines the thickness of the material layer, directly affecting the total volume required.
 Home
Home
 Back
Back