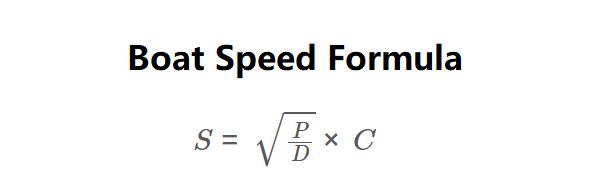Boat Speed Calculator

Power (\( P \)):

Displacement (\( D \)):

Crouch Constant (\( C \)):

1. What is the Boat Speed Calculator?

Definition: This calculator estimates the speed (\( S \)) of a boat using Crouch's formula, based on power (\( P \)), displacement (\( D \)), and a boat-type-specific Crouch constant (\( C \)).

Purpose: It is used by boat enthusiasts, engineers, and designers to predict boat performance under given power and weight conditions.

2. How Does the Calculator Work?

The calculator uses Crouch's formula:

\( S = \sqrt{\frac{P}{D}} \times C \)

Where:

\( S \): Boat speed (mph, km/h, knots, m/s);
\( P \): Power (hp, W, kW, MW converted to hp);
\( D \): Displacement (lbs, kg, t, US ton, long ton converted to lbs);
\( C \): Crouch constant (depends on boat type).

Steps:

Enter the power (\( P \)) with its unit.
Enter the displacement (\( D \)) with its unit.
Select the boat type to determine the Crouch constant (\( C \)).
Convert power to horsepower and displacement to pounds.
Calculate the speed using \( S = \sqrt{\frac{P}{D}} \times C \).
Convert the speed to the selected output unit.
Display the result, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Boat Speed Calculation

Calculating boat speed is essential for:

Performance Optimization: Helps in selecting the right engine for a boat.
Design and Engineering: Assists in designing efficient hulls and propulsion systems.
Recreational Planning: Useful for enthusiasts planning trips or races.

4. Using the Calculator

Example 1: Calculate the speed of a hydroplane with \( P = 3000 \, \text{hp} \), \( D = 6800 \, \text{lbs} \), and \( C = 220 \):

Power: \( P = 3000 \, \text{hp} \);
Displacement: \( D = 6800 \, \text{lbs} \);
Crouch Constant: \( C = 220 \) (hydroplanes);
Speed: \( S = \sqrt{\frac{3000}{6800}} \times 220 \approx 146.13 \, \text{mph} \);
Result (Speed in mph): \( S = 146.1300 \, \text{mph} \);
Result (Speed in km/h): \( S = 235.1379 \, \text{km/h} \);
Result (Speed in knots): \( S = 126.9685 \, \text{knots} \);
Result (Speed in m/s): \( S = 65.3300 \, \text{m/s} \).

Example 2: Calculate the speed of a racing boat with \( P = 373 \, \text{kW} \), \( D = 2 \, \text{t} \), and \( C = 210 \):

Power: \( P = 373 \, \text{kW} \times 1.34102 = 500.39 \, \text{hp} \);
Displacement: \( D = 2 \, \text{t} \times 2204.62 = 4409.24 \, \text{lbs} \);
Crouch Constant: \( C = 210 \) (racing boats);
Speed: \( S = \sqrt{\frac{500.39}{4409.24}} \times 210 \approx 70.57 \, \text{mph} \);
Result (Speed in mph): \( S = 70.5700 \, \text{mph} \);
Result (Speed in km/h): \( S = 113.5785 \, \text{km/h} \);
Result (Speed in knots): \( S = 61.3330 \, \text{knots} \);
Result (Speed in m/s): \( S = 31.5435 \, \text{m/s} \).

5. Frequently Asked Questions (FAQ)

Q: What is Crouch's formula?
A: Crouch's formula (\( S = \sqrt{\frac{P}{D}} \times C \)) estimates a boat's speed based on its power, displacement, and a constant specific to the boat type.

Q: What is the Crouch constant?
A: The Crouch constant (\( C \)) is a value that varies by boat type, reflecting hull design and performance characteristics.

Q: Does this calculator account for water conditions?
A: No, this calculator assumes ideal conditions. Factors like water currents, waves, or wind are not considered.