Angle of Depression Calculator

Calculate:

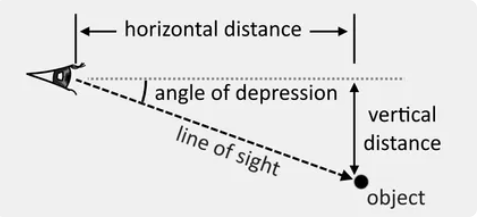
1. What is Angle of Depression Calculator?

Definition: This calculator determines the angle of depression, which is the angle by which a line of sight deviates downward from the horizontal when an observer looks at an object below their level. It can also calculate the vertical or horizontal distance if the angle and one distance are known.

Purpose: It helps users in fields like surveying, aviation, and engineering to calculate angles of depression or distances for navigation, design, and safety purposes.

2. How Does the Calculator Work?

The calculator uses the following equations:

Angle of Depression: \( \theta = \arctan(\text{vertical distance} / \text{horizontal distance}) \)
Vertical Distance: \( \text{vertical distance} = \tan(\theta) \times \text{horizontal distance} \)
Horizontal Distance: \( \text{horizontal distance} = \text{vertical distance} / \tan(\theta) \)

Where:

\( \text{vertical distance} \): The height difference between the observer and the object;
\( \text{horizontal distance} \): The ground distance between the observer and the object;
\( \theta \): The angle of depression (in degrees).

Steps:

Select what you want to calculate: angle of depression, vertical distance, or horizontal distance.
Enter the required inputs (vertical distance, horizontal distance, or angle) and select their units.
Click "Calculate" to compute the result.
For distance results, change the unit using the dropdown to convert the result dynamically.
Results are displayed with 4 decimal places or in scientific notation if less than 0.001.

3. Importance of Angle of Depression Calculation

Calculating the angle of depression is crucial for:

Navigation: Pilots use it to determine landing approaches.
Surveying: Engineers calculate slopes and distances for construction projects.
Safety: Ensures accurate measurements for safe operations at heights.

4. Using the Calculator

Example 1: Calculate the angle of depression (as per Omni Calculator example):

Vertical Distance: 1.5 m;
Horizontal Distance: 3.0 m;
Angle of Depression: \( \theta = \arctan(1.5 / 3.0) \approx 26.5651^\circ \);
Result: Angle of Depression = 26.5651 degrees.

Example 2: Calculate the vertical distance:

Horizontal Distance: 3.0 m;
Angle of Depression: 26.5651 degrees;
Vertical Distance: \( \text{vertical distance} = \tan(26.5651^\circ) \times 3.0 \approx 1.5000 \, \text{m} \);
Result: Vertical Distance = 1.5000 m (can be converted to other units like 150.0000 cm).

Example 3: Calculate the horizontal distance with different units:

Vertical Distance: 50 ft (15.24 m);
Angle of Depression: 30 degrees;
Horizontal Distance: \( \text{horizontal distance} = 15.24 / \tan(30^\circ) \approx 26.3896 \, \text{m} \);
Result: Horizontal Distance = 86.6127 ft (initially displayed as 26.3896 m, converted to feet).

5. Frequently Asked Questions (FAQ)

Q: What is the angle of depression?
A: The angle of depression is the angle between the horizontal line and the line of sight when an observer looks downward at an object below their level.

Q: How is the angle of depression related to the angle of elevation?
A: The angle of depression is equal to the angle of elevation when viewed from the opposite point, as they form alternate angles in a transversal line.

Q: What is the maximum angle of depression?
A: The maximum angle of depression is 90 degrees, which occurs when the object is directly below the observer.