Angle Cut Calculator

Vertical Measurement (\( A \)):

Horizontal Measurement (\( B \)):

Plank Thickness (\( t \)):

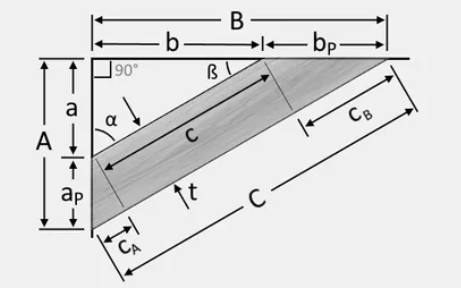
1. What is Angle Cut Calculator?

Definition: This calculator determines the outer length, angles, offsets, and inner part distances required to cut a plank for knee bracing, ensuring it fits flush against a vertical and horizontal member (e.g., a post and beam structure).

Purpose: It helps carpenters and DIY enthusiasts calculate the outer length of the knee bracing, precise cutting angles, offsets for marking cuts, and inner distances in woodworking or steel structures, allowing accurate cutting without a protractor.

2. How Does the Calculator Work?

The calculator uses the following equations:

Outer Length: \( C = \sqrt{A^2 + B^2} \)
Vertical Cut Angle: \( \alpha = \arccos(A / C) \)
Horizontal Cut Angle: \( \beta = 90^\circ - \alpha \)
Offset for Vertical Cut: \( C_A = \frac{t}{\tan(\alpha)} \)
Offset for Horizontal Cut: \( C_B = \frac{t}{\tan(\beta)} \)
Inner Part Distance: \( c = C - C_A - C_B \)
Inner Part Distance (Vertical): \( a = \frac{A}{C} \times c \)
Inner Part Distance (Horizontal): \( b = \frac{B}{C} \times c \)

Where:

\( A \): Vertical measurement from where the post and beam intersect to the tip of the knee bracing attached to the post (converted to mm);
\( B \): Horizontal measurement from where the post and beam intersect to the tip of the knee bracing attached to the beam (converted to mm);
\( C \): Outer length of the knee bracing;
\( t \): Plank thickness (converted to mm);
\( \alpha \): Vertical cut angle (in degrees);
\( \beta \): Horizontal cut angle (in degrees);
\( C_A \): Offset distance for marking the vertical cut;
\( C_B \): Offset distance for marking the horizontal cut;
\( c \): Inner part distance along the hypotenuse;
\( a \): Inner part distance projected vertically;
\( b \): Inner part distance projected horizontally.

Steps:

Enter the vertical measurement (\( A \)) and select its unit.
Enter the horizontal measurement (\( B \)) and select its unit.
Enter the plank thickness (\( t \)) and select its unit.
Click "Calculate" to compute the outer length, angles, offsets, and inner part distances.
Select the desired unit for the output lengths (\( C \), \( C_A \), \( C_B \), \( c \), \( a \), \( b \)).
Results are displayed with 4 decimal places or in scientific notation if less than 0.001.

3. Importance of Angle Cut Calculation

Calculating angle cuts, offsets, and inner distances is crucial for:

Precision: Ensures the plank fits perfectly against the vertical and horizontal members.
Structural Integrity: Provides proper support in framing projects like knee bracing.
Practicality: Allows accurate marking for cuts without needing a protractor, and provides inner distances for further design.

4. Using the Calculator

Example 1: Calculate the outer length, angles, offsets, and inner distances for a knee brace:

Vertical Measurement (\( A \)): 40 cm;
Horizontal Measurement (\( B \)): 30 cm;
Plank Thickness (\( t \)): 10 cm;
Outer Length: \( C = \sqrt{40^2 + 30^2} = 50 \, \text{cm} \);
Vertical Cut Angle: \( \alpha = \arccos(40 / 50) \approx 36.8699^\circ \);
Horizontal Cut Angle: \( \beta = 90^\circ - 36.8699^\circ \approx 53.1301^\circ \);
Offset for Vertical Cut: \( C_A = 10 / \tan(36.8699^\circ) \approx 13.3333 \, \text{cm} \);
Offset for Horizontal Cut: \( C_B = 10 / \tan(53.1301^\circ) \approx 7.5000 \, \text{cm} \);
Inner Part Distance: \( c = 50 - 13.3333 - 7.5000 \approx 29.1667 \, \text{cm} \);
Inner Part Distance (Vertical): \( a = (40 / 50) \times 29.1667 \approx 23.3333 \, \text{cm} \);
Inner Part Distance (Horizontal): \( b = (30 / 50) \times 29.1667 \approx 17.5000 \, \text{cm} \);
Result: Outer Length = 50.0000 cm, Vertical Cut Angle = 36.8699 degrees, Horizontal Cut Angle = 53.1301 degrees, Offset for Vertical Cut = 13.3333 cm, Offset for Horizontal Cut = 7.5000 cm, Inner Part Distance (\( c \)) = 29.1667 cm, Inner Part Distance (\( a \)) = 23.3333 cm, Inner Part Distance (\( b \)) = 17.5000 cm.

Example 2: Calculate with different units:

Vertical Measurement (\( A \)): 16 in (406.4 mm);
Horizontal Measurement (\( B \)): 12 in (304.8 mm);
Plank Thickness (\( t \)): 4 in (101.6 mm);
Outer Length: \( C = \sqrt{406.4^2 + 304.8^2} \approx 508.0 \, \text{mm} \);
Vertical Cut Angle: \( \alpha = \arccos(406.4 / 508.0) \approx 36.8699^\circ \);
Horizontal Cut Angle: \( \beta = 90^\circ - 36.8699^\circ \approx 53.1301^\circ \);
Offset for Vertical Cut: \( C_A = 101.6 / \tan(36.8699^\circ) \approx 135.4667 \, \text{mm} \);
Offset for Horizontal Cut: \( C_B = 101.6 / \tan(53.1301^\circ) \approx 76.2000 \, \text{mm} \);
Inner Part Distance: \( c = 508.0 - 135.4667 - 76.2000 \approx 296.3333 \, \text{mm} \);
Inner Part Distance (Vertical): \( a = (406.4 / 508.0) \times 296.3333 \approx 237.0667 \, \text{mm} \);
Inner Part Distance (Horizontal): \( b = (304.8 / 508.0) \times 296.3333 \approx 177.8000 \, \text{mm} \);
Result (in inches): Outer Length = 20.0000 in, Offset for Vertical Cut = 5.3333 in, Offset for Horizontal Cut = 3.0000 in, Inner Part Distance (\( c \)) = 11.6667 in, Inner Part Distance (\( a \)) = 9.3333 in, Inner Part Distance (\( b \)) = 7.0000 in.

5. Frequently Asked Questions (FAQ)

Q: What is a knee brace?
A: A knee brace is a diagonal structural member that supports two perpendicular members (e.g., a post and beam) to enhance stability.

Q: What are inner part distances?
A: Inner part distances (\( c \), \( a \), \( b \)) represent the lengths of the knee brace after accounting for the offsets at each end, projected along the hypotenuse (\( c \)), vertical (\( a \)), and horizontal (\( b \)) directions.

Q: Can I use this calculator without a protractor?
A: Yes, the calculator provides offset distances (\( C_A \) and \( C_B \)) that you can use to mark your plank for cutting, eliminating the need for a protractor.