1. What is the Unoccupied Wheelchair (3:12) Ramp Slope Calculator?

Definition: This calculator determines the slope angle, elevation grade, run, and ramp length for a ramp with a fixed 3:12 slope ratio, designed for loading and unloading unoccupied wheelchairs.

Purpose: It assists in designing ramps for temporary or specific use cases, such as vehicle loading ramps or storage, where the wheelchair is unoccupied and a steeper slope is acceptable.

2. How Does the Calculator Work?

The calculator uses the following equations for a 3:12 slope ratio (3 units rise per 12 units run, equivalent to 1:4):

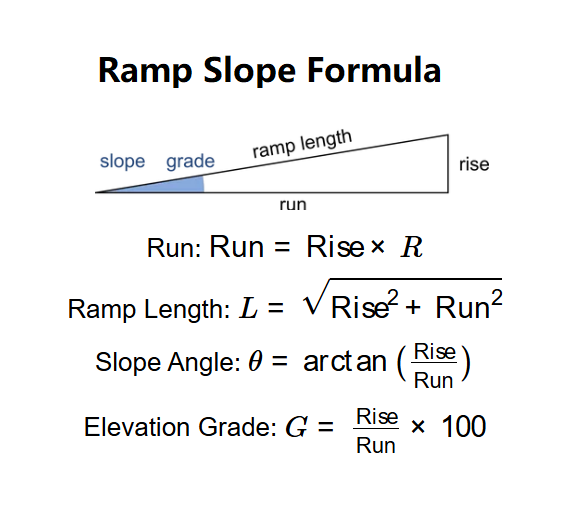
• Run: $\text{Run}=\text{Rise}\times 4$
• Ramp Length: $L=\sqrt{{\text{Rise}}^2+{\text{Run}}^2}$
• Slope Angle: $\theta =\arctan \left(\frac{\text{Rise}}{\text{Run}}\right)$
• Elevation Grade: $G=\frac{\text{Rise}}{\text{Run}}\times 100$

Where:

• $\text{Rise}$: Vertical height to overcome (cm, m, in, ft, or yd);
• $\text{Run}$: Horizontal length (m or ft);
• $L$: Ramp length, the hypotenuse (m or ft);
• $\theta$: Slope angle (degrees);
• $G$: Elevation grade (percent).

Steps:

• Enter the rise and select its unit (cm, m, in, ft, or yd).
• Convert rise to meters for calculations.
• Calculate the run by multiplying rise by 4 (for 3:12 ratio).
• Calculate the ramp length using the Pythagorean theorem.
• Calculate the slope angle using arctangent.
• Calculate the elevation grade as a percentage.
• Convert run and ramp length to the selected output unit (m or ft).
• Display results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Unoccupied Wheelchair (3:12) Slope Calculation

Calculating the correct ramp dimensions for a 3:12 slope is critical for:

• Practicality: Provides a steep incline suitable for temporary or unoccupied wheelchair scenarios, such as loading into vehicles or storage.
• Safety: Ensures the ramp is stable for pushing an unoccupied wheelchair, with a slope of ~14° (25%).
• Space Efficiency: Allows shorter ramps where space is limited and ADA compliance is not required.

4. Using the Calculator

Example: Calculate the ramp parameters for an unoccupied wheelchair slope:

• Rise: $0.5\text{m}$;
• Slope Ratio: 3:12 (Unoccupied Wheelchair);
• Output Unit: Meters;
• Run: $0.5\times 4=2\text{m}$;
• Ramp Length: $\sqrt{{0.5}^2+2^2}\approx 2.0616\text{m}$;
• Slope Angle: $\arctan \left(\frac{0.5}{2}\right)\approx {14.0362}^{\circ }$;
• Elevation Grade: $\frac{0.5}{2}\times 100=25\mathrm{\%}$;
• Result: $\theta ={14.0362}^{\circ },G=25.0000\mathrm{\%},\text{Run}=2.0000\text{m},L=2.0616\text{m}$.

5. Frequently Asked Questions (FAQ)

Q: What does the 3:12 slope ratio mean?
A: A 3:12 ratio means 3 units of rise per 12 units of run (or 1:4), resulting in a slope of approximately 14° or 25%, suitable for loading and unloading unoccupied wheelchairs.

Q: Is the 3:12 slope safe for occupied wheelchairs?
A: No, 3:12 is too steep for occupied wheelchairs and does not meet ADA standards. It is designed for unoccupied wheelchairs during loading or unloading.

Q: Does the calculator account for ramp landings?
A: No, it calculates the straight ramp segment. Landings are typically not required for short, temporary ramps used for unoccupied wheelchairs.

Unoccupied Wheelchair (3:12) Ramp Slope Calculator© - All Rights Reserved 2025