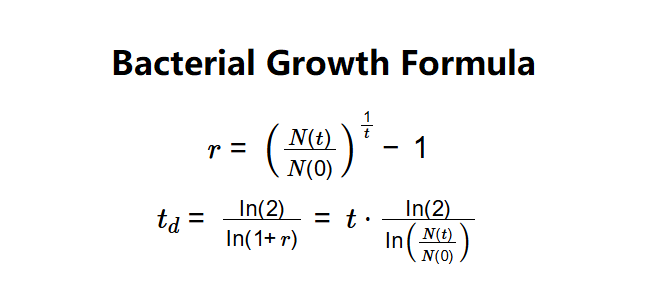Bacterial Growth Rate Calculator

1. What is the Bacterial Growth Rate Calculator?

Definition: This calculator computes the bacterial growth rate (\( r \)) and doubling time (\( t_d \)) based on the initial population (\( N(0) \)), final population (\( N(t) \)), and time interval (\( t \)).

Purpose: It is used in microbiology to quantify how quickly a bacterial population grows, which is critical for studying bacterial behavior, optimizing culture conditions, and understanding microbial dynamics in various environments.

2. How Does the Calculator Work?

The calculator uses the following equations:

\( r = \left( \frac{N(t)}{N(0)} \right)^{\frac{1}{t}} - 1 \)
\( t_d = \frac{\ln(2)}{\ln(1 + r)} = t \cdot \frac{\ln(2)}{\ln \left( \frac{N(t)}{N(0)} \right)} \)

Where:

\( N(0) \): Initial bacterial population;
\( N(t) \): Final bacterial population after time \( t \);
\( t \): Time interval (s, min, hr);
\( r \): Growth rate (unitless);
\( t_d \): Doubling time (s, min, hr).

Steps:

Enter the initial population (\( N(0) \)).
Enter the final population (\( N(t) \)).
Enter the time (\( t \)) with its unit (seconds, minutes, or hours).
Convert the time to hours for calculation.
Calculate the growth rate using the formula.
Calculate the doubling time using the formula.
Convert the doubling time to the selected output unit and display, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Bacterial Growth Rate Calculation

Calculating bacterial growth rate and doubling time is crucial for:

Microbiology Research: Understanding bacterial proliferation under different conditions (e.g., temperature, nutrients).
Biotechnology: Optimizing bacterial cultures for producing antibiotics, enzymes, or other bioproducts.
Public Health: Modeling bacterial growth in infections or contamination scenarios to predict spread and inform control measures.

4. Using the Calculator

Example 1: Calculate the growth rate and doubling time for a bacterial population that grows from 1000 to 4000 in 2 hours:

Initial Population: \( N(0) = 1000 \);
Final Population: \( N(t) = 4000 \);
Time: \( t = 2 \, \text{hr} \);
Growth Rate: \( r = \left( \frac{4000}{1000} \right)^{\frac{1}{2}} - 1 = \sqrt{4} - 1 = 1.0000 \);
Doubling Time: \( t_d = 2 \cdot \frac{\ln(2)}{\ln(4000/1000)} = 2 \cdot \frac{\ln(2)}{\ln(4)} \approx 1.0000 \, \text{hr} \);
Result: \( r = 1.0000 \), \( t_d = 1.0000 \, \text{hr} \).

Example 2: Calculate the growth rate and doubling time for a bacterial population that grows from 500 to 2000 in 180 minutes, outputting doubling time in minutes:

Initial Population: \( N(0) = 500 \);
Final Population: \( N(t) = 2000 \);
Time: \( t = 180 \, \text{min} = 3 \, \text{hr} \);
Growth Rate: \( r = \left( \frac{2000}{500} \right)^{\frac{1}{3}} - 1 = 4^{\frac{1}{3}} - 1 \approx 0.5874 \);
Doubling Time: \( t_d = 3 \cdot \frac{\ln(2)}{\ln(2000/500)} \approx 1.5000 \, \text{hr} = 90.0000 \, \text{min} \);
Result: \( r = 0.5874 \), \( t_d = 90.0000 \, \text{min} \).

5. Frequently Asked Questions (FAQ)

Q: What does the bacterial growth rate tell us?
A: The growth rate (\( r \)) quantifies how quickly the bacterial population increases per unit time, useful for comparing growth under different conditions.

Q: Why is doubling time important?
A: Doubling time (\( t_d \)) indicates the time required for the bacterial population to double, which is key for understanding exponential growth phases.

Q: Does this calculator account for lag or stationary phases?
A: No, this calculator assumes exponential growth. In reality, bacterial growth includes lag, exponential, stationary, and death phases, which may require more complex models.